B&B dan TSP

Back to IF2211 Strategi Algoritma

Topic

Question and Cues

• Apa itu Persoalan TSP?
• Metode 1: Matriks Ongkos Tereduksi
• Apa itu Matriks Tereduksi?
• Langkah-langkah Reduksi Matriks
• Menghitung Batas Bawah (Cost) Simpul Akar
• Formula Cost untuk Simpul Anak
• Prosedur Ekspansi Simpul
• Contoh Lengkap TSP (n=5)
• Langkah 1: Cost Simpul Akar
• Langkah 2: Ekspansi Simpul Akar
• Langkah 3: Ekspansi Simpul-E (Cost Terkecil)
• Langkah 4: Menemukan Solusi Pertama
• Langkah 5: Memangkas Pohon & Kesimpulan
• Latihan TSP (n=4)
• Metode 2: Bobot Tur Lengkap

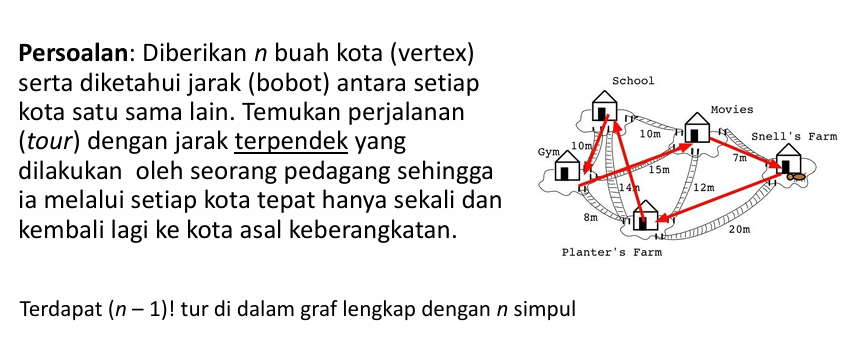
Definisi Traveling Salesperson Problem (TSP):

• Persoalan: Diberikan n buah kota beserta jarak (bobot) antar kota, seorang pedagang harus menemukan rute perjalanan (tur) terpendek.
• Syarat: Tur harus melalui setiap kota tepat satu kali dan kembali ke kota asal.
• Kompleksitas: Untuk graf lengkap dengan n simpul, terdapat (n – 1)! kemungkinan tur. Mencoba semua kemungkinan (brute force) menjadi tidak mungkin untuk n yang cukup besar.

Metode 1: Menggunakan Matriks Ongkos Tereduksi (Reduced Cost Matrix)

Ini adalah pendekatan B&B yang sistematis untuk menghitung batas bawah (lower bound) dari biaya tur pada setiap simpul di pohon ruang status.

• Konsep Matriks Tereduksi:
  • Sebuah matriks biaya (ongkos) dikatakan tereduksi jika setiap baris dan setiap kolomnya memiliki paling sedikit satu elemen bernilai nol (0), dan semua elemen lainnya bernilai non-negatif. Logika: Mengurangi semua elemen di satu baris atau kolom dengan nilai konstanta t akan mengurangi total biaya setiap tur yang mungkin sebesar t. Dengan melakukan ini, kita bisa mendapatkan matriks yang lebih sederhana (memiliki banyak nol) tanpa mengubah solusi optimal relatifnya. Total nilai pengurang ini menjadi dasar perhitungan lower bound.
• Langkah-langkah Reduksi Matriks (untuk Simpul Akar):
  1. Reduksi Baris: Untuk setiap baris, cari elemen terkecil, lalu kurangkan semua elemen di baris tersebut dengan nilai terkecil itu. Jumlahkan semua nilai pengurang dari setiap baris.
  2. Reduksi Kolom: Setelah reduksi baris, lakukan hal yang sama untuk setiap kolom pada matriks hasil. Cari elemen terkecil di setiap kolom, kurangkan semua elemen di kolom itu dengan nilai tersebut. Jumlahkan semua nilai pengurang dari setiap kolom.
  3. Hasil: Matriks yang didapat sekarang adalah matriks tereduksi.
• Menghitung Batas Bawah (Cost) Simpul Akar ĉ(akar):
  • Nilai lower bound untuk simpul akar (sebelum ada perjalanan yang dipilih) adalah jumlah total semua nilai pengurang dari proses reduksi baris dan kolom.
  • ĉ(akar) = (Total Pengurang Baris) + (Total Pengurang Kolom)
• Formula Perhitungan Cost untuk Simpul Anak:
  • Misalkan kita akan berekspansi dari simpul R ke simpul anak S dengan memilih lintasan (sisi) (i, j). A adalah matriks tereduksi milik simpul R.
  • Formula cost untuk simpul anak S adalah: $\hat{c}(S)=\hat{c}(R)+A(i,j)+r$
    • ĉ(R): Cost dari simpul induk R.
    • A(i, j): Nilai biaya dari sisi (i, j) pada matriks tereduksi milik induk R.
    • r: Jumlah total pengurang baru yang didapat dari mereduksi matriks untuk simpul S.
• Prosedur Ekspansi Simpul (dari R ke S melalui sisi (i, j)):
  1. Ambil matriks tereduksi dari simpul R.
  2. Ubah Baris i dan Kolom j menjadi ∞: Ini untuk memastikan kita tidak akan keluar dari kota i lagi atau masuk ke kota j lagi.
  3. Cegah Sub-tur: Ubah elemen matriks A(j, 1) menjadi ∞ (dengan asumsi kota awal adalah 1). Ini mencegah terbentuknya tur prematur seperti 1 -> j -> 1 sebelum semua kota lain dikunjungi.
  4. Reduksi Kembali: Lakukan proses reduksi baris dan kolom pada matriks yang baru diubah ini. Jumlah total pengurangnya adalah nilai r.
  5. Hitung ĉ(S) menggunakan formula di atas.
• Contoh Lengkap Penyelesaian TSP (n=5):
  • Matriks Awal:

          1    2    3    4    5
    1   inf   20   30   10   11
    2   15   inf   16    4    2
    3    3    5   inf    2    4
    4   19    6   18   inf    3
    5   16    4    7   16   inf
    

• Langkah 1: Menghitung Cost Simpul Akar (Simpul 1):
  1. Reduksi Baris:
     • Baris 1: kurangi 10 → (inf, 10, 20, 0, 1)
     • Baris 2: kurangi 2 → (13, inf, 14, 2, 0)
     • Baris 3: kurangi 2 → (1, 3, inf, 0, 2)
     • Baris 4: kurangi 3 → (16, 3, 15, inf, 0)
     • Baris 5: kurangi 4 → (12, 0, 3, 12, inf)
     • Total Pengurang Baris = 10 + 2 + 2 + 3 + 4 = 21
  2. Reduksi Kolom (pada matriks hasil reduksi baris):
     • Kolom 1: kurangi 1
     • Kolom 3: kurangi 3
     • (Kolom 2, 4, 5 sudah punya 0)
     • Total Pengurang Kolom = 1 + 0 + 3 + 0 + 0 = 4
  3. Cost Simpul Akar: ĉ(1) = 21 + 4 = 25.
  4. Matriks Tereduksi Awal (Matriks A):

           1    2    3    4    5
     1   inf   10   17    0    1
     2   12   inf   11    2    0
     3    0    3   inf    0    2
     4   15    3   12   inf    0
     5   11    0    0   12   inf
     

• Langkah 2: Ekspansi Simpul Akar (Simpul 1):
  • Kita hitung cost untuk setiap anak simpul akar (tur dari 1 ke 2, 1 ke 3, dst).
  • Ke Simpul 2 (lintasan 1→2): ĉ(2) = ĉ(1) + A(1,2) + r = 25 + 10 + 0 = 35. (r=0 karena matriks setelah modifikasi sudah tereduksi).
  • Ke Simpul 3 (lintasan 1→3): ĉ(3) = ĉ(1) + A(1,3) + r = 25 + 17 + 11 = 53.
  • Ke Simpul 4 (lintasan 1→4): ĉ(4) = ĉ(1) + A(1,4) + r = 25 + 0 + 0 = 25.
  • Ke Simpul 5 (lintasan 1→5): ĉ(5) = ĉ(1) + A(1,5) + r = 25 + 1 + 5 = 31.
  • Pohon Saat Ini: Simpul hidup: {2(35), 3(53), 4(25), 5(31)}.
• Langkah 3: Ekspansi Simpul-E Berikutnya:
  • Simpul-E (Expand) adalah simpul hidup dengan cost terkecil: Simpul 4 (cost 25).
  • Ekspansi dari Simpul 4 (lintasan 1→4). Matriksnya adalah matriks A yang dimodifikasi (baris 1, kolom 4 di-set inf).
  • Anak dari Simpul 4:
    • Ke Simpul 6 (lintasan 1→4→2): ĉ(6) = ĉ(4) + B(4,2) + r = 25 + 3 + 0 = 28.
    • Ke Simpul 7 (lintasan 1→4→3): ĉ(7) = ĉ(4) + B(4,3) + r = 25 + 12 + 13 = 50. (Mengikuti nilai r dari sumber).
    • Ke Simpul 8 (lintasan 1→4→5): ĉ(8) = ĉ(4) + B(4,5) + r = 25 + 0 + 11 = 36. (Mengikuti nilai r dari sumber).
  • Pohon Saat Ini: Simpul hidup: {2(35), 3(53), 5(31), 6(28), 7(50), 8(36)} .
  • Simpul-E berikutnya: Simpul 6 (cost 28).
  • Ekspansi dari Simpul 6 (lintasan 1→4→2).
  • Anak dari Simpul 6:
    • Ke Simpul 10 (lintasan 1→4→2→5): ĉ(10) = ĉ(6) + C(2,5) + r = 28 + 0 + 0 = 28.
  • Proses ini terus berlanjut…
• Langkah 4: Menemukan Solusi Pertama (Simpul Daun):
  • Setelah beberapa ekspansi, kita mencapai Simpul 11 (lintasan 1→4→2→5→3). Ini adalah simpul daun karena semua kota telah dikunjungi.
  • ĉ(11) = 28. Ini adalah tur lengkap pertama yang kita temukan: 1→4→2→5→3→1 dengan total bobot 28.
  • Nilai 28 sekarang menjadi Upper Bound (U), yaitu solusi terbaik sejauh ini.
• Langkah 5: Memangkas Pohon dan Kesimpulan:

  • Sekarang kita periksa semua simpul hidup yang tersisa di priority queue: {2(35), 3(53), 5(31), 7(50), 8(36), 9(52)}.

  • Semua simpul hidup ini memiliki ĉ(i) yang lebih besar atau sama dengan solusi terbaik kita (U=28). Artinya, tidak ada satupun dari cabang-cabang ini yang bisa menghasilkan tur dengan biaya < 28.

  • Oleh karena itu, semua simpul hidup tersebut dipangkas (dibunuh).

  • Karena tidak ada lagi simpul hidup untuk dieksplorasi, algoritma berhenti.

  • Solusi Optimal: Tur 1→4→2→5→3→1 dengan total bobot 28.

Metode 2: Cost Berdasarkan Bobot Tur Lengkap:

• Ini adalah pendekatan heuristik lain untuk menghitung lower bound.
• Prinsip: Biaya tur manapun setidaknya adalah setengah dari jumlah bobot dua sisi termurah yang terhubung ke setiap kota.
• Formula Batas Bawah Awal: $\text{Lower Bound}\ge \frac{1}{2}{\sum }_{v\in V}(\text{bobot sisi termurah dari v}+\text{bobot sisi kedua termurah dari v})$
• Proses:
  1. Hitung lower bound awal menggunakan formula di atas. Ini menjadi cost simpul akar.
  2. Saat kita memilih sebuah sisi (misal (a, c)) untuk dimasukkan ke dalam tur, kita membuat perhitungan lower bound yang baru untuk simpul anak.
  3. Perhitungan baru ini tetap menggunakan prinsip yang sama, namun sekarang dengan “paksaan” bahwa sisi (a, c) harus ada dalam perhitungan untuk simpul a dan c.

Summary

Untuk menyelesaikan TSP, algoritma Branch & Bound secara sistematis membangun pohon ruang status dari semua kemungkinan tur parsial. Kunci efisiensinya terletak pada perhitungan lower bound (batas bawah biaya) yang ketat untuk setiap tur parsial. Metode utama, Matriks Ongkos Tereduksi, secara algoritmik menghitung batas bawah ini dengan mengakumulasi total nilai reduksi dari matriks biaya. Dengan selalu mengeksplorasi tur parsial yang memiliki lower bound terkecil dan memangkas cabang yang biayanya sudah melebihi solusi terbaik yang ditemukan, B&B dapat menemukan tur optimal tanpa harus memeriksa seluruh (n-1)! kemungkinan.

Additional Information (Optional)

Aspek Teknis Lanjutan:

• Algoritma Held-Karp: Batas bawah yang dijelaskan dalam “Bobot Tur Lengkap” adalah versi sederhana dari ide yang jauh lebih kuat yang disebut Held-Karp Lower Bound. Algoritma Held-Karp menghasilkan batas bawah yang sangat ketat (seringkali sangat dekat dengan solusi optimal) dengan menggunakan konsep Minimum 1-Trees. Sebuah 1-Tree adalah sebuah Minimum Spanning Tree (MST) pada n-1 kota, yang kemudian dihubungkan ke kota sisa dengan dua sisi termurah. Ini adalah salah satu batas bawah paling terkenal dan efektif untuk TSP.
• Simetris vs. Asimetris TSP: Contoh di atas adalah untuk TSP simetris (jarak(i, j) = jarak(j, i)). Metode Matriks Ongkos Tereduksi berfungsi dengan sempurna juga untuk TSP asimetris (misalnya, jarak(i, j) merepresentasikan biaya tiket pesawat yang bisa berbeda arah), di mana matriks biayanya tidak simetris.
• Kekompleksan B&B untuk TSP: Meskipun B&B secara signifikan lebih baik daripada brute force, pada kasus terburuknya (worst case), ia masih memiliki kompleksitas eksponensial. Performanya di dunia nyata sangat bergantung pada kualitas lower bound yang digunakan dan struktur dari masalah spesifik.

Sumber & Referensi Lanjutan:

• Publikasi Ilmiah: “The traveling-salesman problem and minimum spanning trees” oleh M. Held dan R. M. Karp (1970). Ini adalah paper seminal yang memperkenalkan Held-Karp bound.
• Buku: Combinatorial Optimization: Algorithms and Complexity oleh Christos H. Papadimitriou dan Kenneth Steiglitz. Menyediakan pembahasan mendalam tentang TSP dan algoritma optimisasi lainnya.

Eksplorasi Mandiri:

• Implementasi: Tantang diri Anda untuk mengimplementasikan B&B dengan metode Matriks Ongkos Tereduksi untuk TSP. Ini adalah proyek pemrograman yang sangat baik untuk memahami algoritma secara mendalam.
• Bandingkan dengan Heuristik: Implementasikan algoritma heuristik sederhana untuk TSP seperti Nearest Neighbor (di setiap langkah, pergi ke kota terdekat yang belum dikunjungi). Bandingkan kecepatan dan kualitas solusi yang dihasilkan oleh heuristik ini dengan solusi optimal yang ditemukan oleh B&B. Anda akan melihat trade-off antara kecepatan dan optimalitas.