IF Notes

Pencarian Tak Terinformasi (Uninformed Search)

6 min read

Back to IF2211 Strategi Algoritma

Topic

Questions/Cues

  • Definisi Masalah & Peta
  • Strategi Uninformed Search
  • BFS: Mekanisme & Contoh
  • BFS: Lacak Simulasi Lengkap
  • DFS: Mekanisme & Contoh
  • DFS: Lacak Simulasi Lengkap
  • IDS: Mekanisme & Contoh
  • IDS: Lacak Iterasi Lengkap
  • Motivasi untuk UCS
  • UCS: Mekanisme & Fungsi g(n)
  • UCS: Lacak Simulasi Lengkap
  • Hasil Optimal UCS

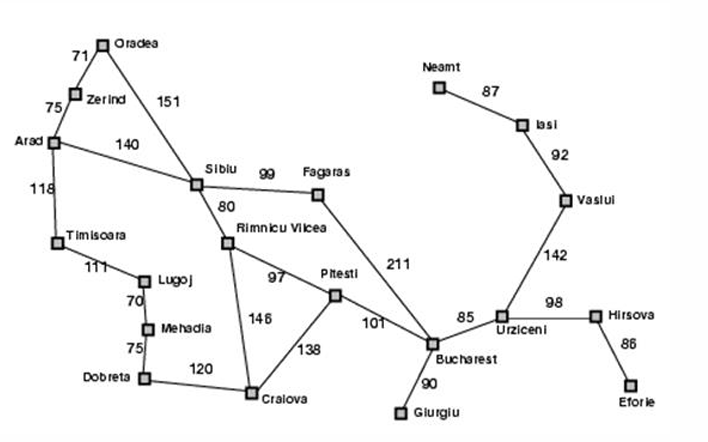
Definisi Masalah Penentuan Rute

  • Persoalan: Diberikan sebuah graf yang merepresentasikan kota-kota dan jaraknya, carilah lintasan terpendek dari kota awal ke kota tujuan.
  • Contoh Konkret (Peta Romania):
    • Himpunan Status (S): Semua kota di peta (Arad, Timisoara, Sibiu, Bucharest, dll.).
    • Status Awal (i.s): Kota Arad (A).
    • Status Tujuan (g.s): Kota Bucharest (B).
    • Tes Tujuan: Apakah simpul saat ini == Bucharest?
    • Biaya Lintasan (Path Cost): Jarak (km) antar kota.

Strategi Pencarian Tak Berinformasi (Uninformed / Blind Search)

Sekelompok algoritma yang menjelajahi ruang status tanpa informasi tambahan tentang lokasi atau kedekatan tujuan. Penjelajahan bersifat sistematis berdasarkan struktur graf saja. Algoritma dalam kategori ini meliputi: BFS, DFS, DLS, IDS, dan UCS.

Breadth-First Search (BFS):

  • Mekanisme: Mengeksplorasi simpul secara lapis demi lapis (level by level). Menggunakan struktur data queue (FIFO: First-In, First-Out).

  • Hasil pada Contoh: Menemukan jalur A → S → F → B dengan total biaya 450. Jalur ini memiliki jumlah langkah (edges) tersedikit, namun bukan jarak terpendek.

  • BFS: Lacak Simulasi Lengkap:
    • “Agenda” diperlakukan sebagai queue. Simpul-E adalah simpul yang diekspansi. Simpul Hidup adalah isi dari queue.
Simpul-ESimpul Hidup (Isi Queue)
A[ZA, SA, TA]
ZA[SA, TA, OAZ]
SA[TA, OAZ, OAS, FAS, RAS]
TA[OAZ, OAS, FAS, RAS, LAT]
OAZ[OAS, FAS, RAS, LAT]
OAS[FAS, RAS, LAT]
FAS[RAS, LAT, BASF]
RAS[LAT, BASF, DASR, CASR, PASR]
LAT[BASF, DASR, CASR, PASR, MATL]
…(Pencarian berlanjut hingga Bucharest ditemukan)

Depth-First Search (DFS):

  • Mekanisme: Mengeksplorasi satu cabang sedalam mungkin sebelum melakukan backtrack. Menggunakan struktur data stack (LIFO: Last-In, First-Out).
  • Hasil pada Contoh: Dapat menemukan jalur yang sangat panjang dan tidak optimal, seperti A → Z → O → S → F → B dengan total biaya 607.
  • DFS: Lacak Simulasi Lengkap:
    • “Agenda” diperlakukan sebagai stack.
Simpul-ESimpul Hidup (Isi Stack)
A[ZA, SA, TA]
ZA[OAZ, SA, TA]
OAZ[SAZO, SA, TA]
SAZO[FAZOS, RAZOS, SA, TA]
FAZOS[BAZOSF, RAZOS, SA, TA]
…(Pencarian berlanjut hingga menemukan solusi atau jalan buntu)

Iterative Deepening Search (IDS):

  • Mekanisme: Menggabungkan keunggulan BFS (optimalitas pada biaya seragam) dan DFS (efisiensi memori). IDS melakukan serangkaian DFS dengan batas kedalaman yang terus meningkat.

  • Hasil pada Contoh: Akan menemukan solusi yang sama dengan BFS, yaitu A → S → F → B.

  • IDS: Lacak Iterasi Lengkap:

    • Depth = 0: A → cutoff (batas kedalaman tercapai).
    • Depth = 1: A → [ZA, SA, TA]
      • Ekspansi ZA → cutoff.
      • Ekspansi SA → cutoff.
      • Ekspansi TA → cutoff.
    • Depth = 2: A → [ZA, SA, TA]
      • Ekspansi ZA → [OAZ] → cutoff.
      • Ekspansi SA → [OAS, FAS, RAS] → OAS: cutoff, FAS: cutoff, RAS: cutoff.
      • Ekspansi TA → [LAT] → cutoff.
    • Depth = 3: A → ZA → OAZ → SAZO → cutoff. … (dan seterusnya hingga) A → SA → FAS → BASF (Solusi ditemukan).

Motivasi untuk Uniform Cost Search (UCS):

  • Algoritma BFS, DFS, dan IDS tidak mempertimbangkan biaya (jarak) dari setiap langkah. Mereka mengasumsikan semua langkah sama.
  • Dalam masalah penentuan rute, tujuan kita adalah mencari path terpendek berdasarkan total jarak, bukan jumlah langkah. Di sinilah UCS diperlukan.

Uniform Cost Search (UCS): Mekanisme & Fungsi g(n)

  • g(n): Didefinisikan sebagai biaya lintasan aktual dari simpul awal (root) ke simpul n.
  • Mekanisme: UCS adalah varian dari BFS yang memprioritaskan simpul untuk dieksplorasi berdasarkan nilai g(n) terendah. Ia selalu memilih jalur termurah dari titik awal. Menggunakan priority queue.
  • Hasil pada Contoh: Menemukan jalur yang benar-benar optimal berdasarkan jarak.
  • UCS: Lacak Simulasi Lengkap:
    • “Agenda” diperlakukan sebagai priority queue yang diurutkan berdasarkan g(n).
Simpul-ESimpul Hidup (Isi Priority Queue)
A[ZA-75, TA-118, SA-140]
ZA-75[TA-118, SA-140, OAZ-146]
TA-118[SA-140, OAZ-146, LAT-229]
SA-140[OAZ-146, RAS-220, LAT-229, FAS-239, OAS-291]
OAZ-146[RAS-220, LAT-229, FAS-239, OAS-291]
RAS-220[LAT-229, FAS-239, OAS-291, PASR-317, DASR-340, CASR-366]
LAT-229[FAS-239, OAS-291, MATL-299, PASR-317, DASR-340, CASR-366]
FAS-239[OAS-291, MATL-299, PASR-317, DASR-340, CASR-366, BASF-450]
OAS-291[MATL-299, PASR-317, DASR-340, CASR-366, BASF-450]
MATL-299[PASR-317, DASR-340, DATLM-364, CASR-366, BASF-450]
PASR-317[DASR-340, DATLM-364, CASR-366, BASRP-418, CASRP-455, BASF-450]
DASR-340[DATLM-364, CASR-366, BASRP-418, CASRP-455, BASF-450]
DATLM-364[CASR-366, BASRP-418, CASRP-455, BASF-450]
CASR-366[BASRP-418, CASRP-455, BASF-450]
  • Hasil Optimal UCS:
    • Dari jejak simulasi di atas, simpul berikutnya yang akan diekspansi adalah BASRP-418. Ini adalah jalur solusi.
    • Jalur Optimal: A → S → R → P → B
    • Total Biaya (Jarak): 418

Ringkasan:

Ad Libitum: Pendalaman Teknis

**

Summary

Strategi Uninformed Search menjelajahi graf secara sistematis. BFS dan DFS, yang beroperasi berdasarkan struktur antrian dan tumpukan, tidak cocok untuk mencari jarak terpendek pada graf dengan biaya bervariasi. Iterative Deepening Search (IDS) mengoptimalkan penggunaan memori, namun masih berorientasi pada jumlah langkah. Untuk menemukan rute dengan total biaya riil terendah, Uniform Cost Search (UCS) adalah metode yang tepat dan dijamin optimal, karena ia secara cerdas memprioritaskan eksplorasi pada jalur dengan total biaya kumulatif g(n) terendah dari titik awal, seperti yang ditunjukkan oleh penemuan jalur A→S→R→P→B (biaya 418) yang lebih murah daripada jalur BFS A→S→F→B (biaya 450).

Graph View

Backlinks