Definisi Formal PDA

Back to IF2224 Teori Bahasa Formal dan Otomata

Pushdown Automata (PDA): Pengenalan, Definisi, & Komputasi

Questions/Cues

• Apa itu Pushdown Automata (PDA)?

• Bagaimana cara kerja PDA?

• Contoh: Bahasa $L_{wwr}$ (Palindrom)

• Bagaimana PDA untuk $L_{wwr}$ bekerja?

• Apa definisi formal PDA (7-tuple)?

• Menjelaskan fungsi transisi ($\delta$)

• Apa itu Instantaneous Descriptions (ID)?

• Notasi $⊢$ dan ${⊢}^{\ast }$

• Apa properti (Teorema 6.5 & 6.6) dari komputasi ID?

Reference Points

• Slide 11_2023_Pushdown Automata.pdf (hlm. 1-11)

Apa itu Pushdown Automata (PDA)?

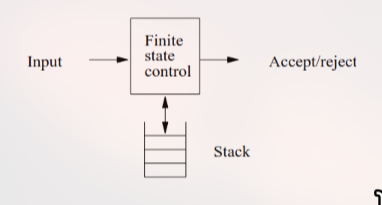
Pushdown Automata (PDA) adalah model komputasi yang lebih kuat daripada Finite Automata (FA).

Pada dasarnya, PDA = NFA + Stack.

• NFA (Non-deterministic Finite Automata): Memiliki finite state control (kontrol state terbatas) dan bisa “menebak” (non-determinisme).

• Stack: Ini adalah memori tambahan. Stack adalah struktur data LIFO (Last-In, First-Out). Ini memberikan PDA kemampuan untuk “mengingat” urutan simbol tanpa batas, sesuatu yang tidak bisa dilakukan NFA.

Bagaimana Cara Kerja PDA?

Dalam setiap langkah (transisi), PDA melakukan tiga hal secara bersamaan:

1. Membaca Input: Membaca simbol input berikutnya (atau $ϵ$, yang berarti transisi spontan tanpa membaca input).

2. Mengubah State: Pindah ke state baru (atau bisa tetap di state yang sama).

3. Memanipulasi Stack: Mengganti simbol di puncak (top) stack dengan sebuah string baru (yang bisa berisi 0, 1, atau banyak simbol).

   • Jika string baru = $ϵ$ (string kosong): Ini adalah operasi POP (menghapus top stack).

   • Jika string baru = simbol top lama + simbol baru: Ini adalah operasi PUSH (menambahkan simbol baru di atas).

   • Jika string baru = simbol top lama: Stack tidak berubah.

Contoh: Bahasa $L_{wwr}$ (Palindrom)

Mari kita tinjau bahasa $L_{wwr}=\{w{w}^R:w\in \{0,1{\}}^{\ast }\}$.

• $w$ adalah string apapun dari 0 dan 1 (misal: “010”).

• $w^R$ adalah kebalikan (reverse) dari $w$ (misal: “010”).

• $w{w}^R$ adalah gabungannya (misal: “010010”). Ini adalah bahasa palindrom dengan panjang genap.

Bahasa ini tidak bisa dikenali oleh NFA biasa karena NFA tidak bisa mengingat seluruh bagian $w$ untuk dicocokkan dengan $w^R$. PDA bisa, menggunakan stack-nya.

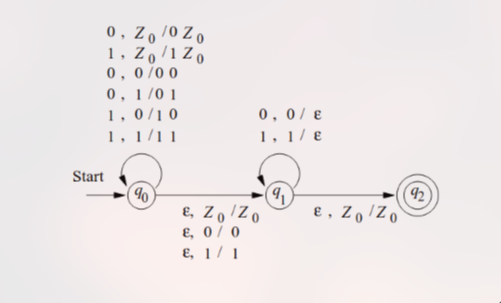
Bagaimana PDA untuk $L_{wwr}$ bekerja?

PDA ini menggunakan non-determinisme untuk “menebak” di mana titik tengah string (batas antara $w$ dan $w^R$).

1. Fase 1: Membaca $w$ (State $q_0$)

   • PDA “menebak” bahwa ia masih membaca bagian $w$.
   • Setiap kali membaca simbol input (0 atau 1), ia PUSH simbol itu ke dalam stack.
   • Contoh: Input “0110”. - Baca ‘0’, push ‘0’. Stack: [0, $Z_0$] - Baca ‘1’, push ‘1’. Stack: [1, 0, $Z_0$]

2. Fase 2: Menebak Titik Tengah (Transisi $q_0\to q_1$)

   • Kapanpun (secara non-deterministik), PDA bisa “menebak” bahwa ia telah mencapai akhir $w$ dan akan mulai membaca $w^R$.

   • Ia melakukan ini dengan transisi spontan (input $ϵ$) dari state $q_0$ ke state $q_1$ tanpa mengubah stack.

3. Fase 3: Membaca $w^R$ (State $q_1$)

   • Sekarang PDA berada di state $q_1$, ia mulai mencocokkan input dengan isi stack.

   • Jika simbol input cocok dengan simbol di top stack, PDA akan POP stack.

   • Contoh (lanjutan): Stack: [1, 0, $Z_0$] - Baca ‘1’, top stack ‘1’. Cocok! Pop stack. Stack: [0, $Z_0$] - Baca ‘0’, top stack ‘0’. Cocok! Pop stack. Stack: [$Z_0$]

   • Jika input atau top stack tidak cocok, komputasi di jalur itu “mati”.

4. Fase 4: Penerimaan (Acceptance) (Transisi $q_1\to q_2$)

   • Setelah semua input habis, jika stack kosong (hanya tersisa simbol awal $Z_0$), berarti seluruh $w$ telah berhasil dicocokkan dengan $w^R$.
   • PDA melakukan transisi spontan (input $ϵ$) ke accept state $q_2$.

Apa definisi formal PDA (7-tuple)?

PDA secara formal didefinisikan sebagai 7-tuple: $P=(Q,\Sigma ,\Gamma ,\delta ,q_0,Z_0,F)$

• $Q$: Himpunan state (terbatas), misal $\{q_0,q_1,q_2\}$.

• $\Sigma$: Alfabet input (terbatas), misal $\{0,1\}$.

• $\Gamma$: Alfabet stack (terbatas), misal $\{0,1,Z_0\}$.

• $\delta$: Fungsi transisi (dijelaskan di bawah).

• $q_0$: Start state.

• $Z_0$: Simbol awal stack (penanda bahwa stack awalnya kosong).

• $F$: Himpunan accepting state, misal $\{q_2\}$.

Menjelaskan Fungsi Transisi ($\delta$)

Ini adalah bagian paling penting. Fungsinya memetakan:

$\delta :Q\times (\Sigma \cup \{ϵ\})\times \Gamma \to 2^{Q\times {\Gamma }^{\ast }}$

Mari kita bedah:

• Input: $(q,a,X)$

  • $q$: State saat ini.

  • $a$: Simbol input yang dibaca (bisa $ϵ$).

  • $X$: Simbol di top stack.

• Output: $2^{Q\times {\Gamma }^{\ast }}$

  • Ini adalah himpunan dari pasangan (state baru, string baru). Himpunan berarti bisa ada beberapa kemungkinan (non-determinisme).

  • $(p,\alpha )$:

    • $p$: State baru.

    • $\alpha$: String yang akan menggantikan $X$ di stack.

Contoh Transisi $L_{wwr}$:

1. $\delta (q_0,0,Z_0)=\{(q_0,0Z_0)\}$

   • (Di $q_0$, baca ‘0’, top stack $Z_0$) $\to$ (Tetap di $q_0$, ganti $Z_0$ dengan $0Z_0$. Efek: push ‘0’).

2. $\delta (q_0,ϵ,Z_0)=\{(q_1,Z_0)\}$

   • (Di $q_0$, baca $ϵ$, top stack $Z_0$) $\to$ (Pindah ke $q_1$, stack tidak berubah. Ini adalah tebakan titik tengah).

3. $\delta (q_1,0,0)=\{(q_1,ϵ)\}$

   • (Di $q_1$, baca ‘0’, top stack ‘0’) $\to$ (Tetap di $q_1$, ganti ‘0’ dengan $ϵ$. Efek: pop ‘0’).

Apa itu Instantaneous Descriptions (ID)?

ID adalah “snapshot” atau konfigurasi PDA pada satu waktu. Ini adalah cara formal untuk melacak komputasi.

ID adalah sebuah triple: $(q,w,\gamma )$

• $q$: State PDA saat ini.

• $w$: Sisa string input yang belum dibaca.

• $\gamma$: Seluruh isi stack, dengan simbol teratas ada di paling kiri.

Notasi $⊢$ dan ${⊢}^{\ast }$

• $⊢$ (“yields”): Menunjukkan satu langkah komputasi.

  • Kita menulis $(q,aw,X\beta )⊢(p,w,\alpha \beta )$

  • Ini berarti ada transisi $\delta (q,a,X)$ yang mengandung $(p,\alpha )$.

  • PDA di state $q$, membaca $a$, dengan sisa input $w$. Top stack adalah $X$ dengan sisa $\beta$.

  • PDA bergerak ke state $p$, sisa input $w$. Top stack $X$ diganti $\alpha$, sehingga stack menjadi $\alpha \beta$.

• ${⊢}^{\ast }$ (“yields in 0 or more steps”):

  • Ini adalah reflexive-transitive closure dari $⊢$.

  • $(q_1,w_1,{\gamma }_1){⊢}^{\ast }(q_k,w_k,{\gamma }_k)$ berarti ada serangkaian langkah (bisa 0, 1, atau lebih) yang membawa PDA dari konfigurasi pertama ke konfigurasi kedua.

Apa properti (Teorema 6.5 & 6.6) dari komputasi ID?

Ini adalah teorema formal tentang bagaimana komputasi berperilaku.

• Theorem 6.5: Jika $(q,x,\alpha ){⊢}^{\ast }(p,y,\beta )$, maka kita bisa menambahkan “ekor” input ($w$) dan “dasar” stack ($\gamma$) yang sama, dan komputasinya tetap valid:

  • $(q,xw,\alpha \gamma ){⊢}^{\ast }(p,yw,\beta \gamma )$

  • Artinya: Komputasi PDA hanya peduli pada bagian atas stack dan awalan input yang dibacanya. Apa yang ada di “dasar” stack atau “akhir” input tidak akan mengganggu komputasi yang sudah terjadi.

• Theorem 6.6: Jika $(q,xw,\alpha ){⊢}^{\ast }(p,yw,\beta )$ (di mana $w$ tidak pernah tersentuh), maka $w$ bisa dihilangkan:

  • $(q,x,\alpha ){⊢}^{\ast }(p,y,\beta )$
  • Artinya: Jika sebuah komputasi berhasil tanpa pernah membaca bagian akhir dari input, komputasi itu juga valid untuk input yang sudah dipotong (tanpa bagian akhir itu).

Summary

Pushdown Automata (PDA) adalah NFA yang diperkuat dengan memori stack (LIFO), yang memungkinkannya untuk mengenali Bahasa Bebas Konteks (Context-Free Languages) seperti palindrom $L_{wwr}$. PDA bekerja dengan membaca input, mengubah state, dan memanipulasi stack (push/pop). Perilaku ini didefinisikan secara formal oleh 7-tuple, terutama fungsi transisi $\delta$ yang bersifat non-deterministik. Untuk melacak proses komputasinya, kita menggunakan Instantaneous Descriptions (ID) yang merepresentasikan snapshot dari (state, sisa input, isi stack) pada satu waktu.

Additional Information

Pendalaman: Non-Determinisme adalah Kunci

Kunci dari PDA $L_{wwr}$ adalah non-determinisme. Ada dua transisi dari $q_0$ ketika top stack adalah $0$:

1. $\delta (q_0,0,0)=\{(q_0,00)\}$ (PUSH - tebak masih di $w$)

2. $\delta (q_0,ϵ,0)=\{(q_1,0)\}$ (Pindah state - tebak sudah di $w^R$)

Ketika PDA berada di $q_0$ dan membaca ‘0’, ia akan “mencabang” komputasinya. Satu cabang akan mengambil transisi 1 (tetap di $q_0$, push ‘0’), dan cabang lainnya akan mengambil transisi 2 (pindah ke $q_1$, stack tetap).

Sebuah string diterima jika setidaknya satu dari semua kemungkinan cabang komputasi ini berakhir di accept state setelah semua input habis. Jika semua cabang “mati” (karena input tidak cocok dengan stack, dll), string ditolak.

Pendalaman: Kekuatan ${\Gamma }^{\ast }$ dalam $\delta$

Fungsi transisi $\delta (q,a,X)\to (p,\alpha )$ di mana $\alpha \in {\Gamma }^{\ast }$ (string dari simbol stack) sangat kuat:

• Jika $\alpha =ϵ$ (string kosong) $\to$ Ini adalah POP.

• Jika $\alpha =X$ $\to$ Stack tidak berubah.

• Jika $\alpha =YX$ $\to$ Ini mengganti $X$ dengan $YX$. Efeknya adalah PUSH $Y$ di atas $X$.

• Jika $\alpha =YZX$ $\to$ Ini mengganti $X$ dengan $YZX$. Efeknya adalah PUSH $Y$ lalu PUSH $Z$. (Atau bisa dilihat sebagai “mengganti $X$ dengan string $YZX$”).

Eksplorasi Mandiri

• Coba lacak komputasi (buat urutan ID) untuk PDA $L_{wwr}$ dengan input “0110”.

• Coba lacak komputasi untuk input “010” (harus ditolak). Di mana komputasinya “mati”?

• Bagaimana Anda memodifikasi PDA ini untuk menerima $L_{wcwR}$ (misal “01c10”)? (Petunjuk: transisi $c$ adalah penanda titik tengah, tidak perlu menebak).

Sumber & Referensi Lanjutan:

• Buku: “Introduction to the Theory of Computation” oleh Michael Sipser (Chapter 2, Bagian “Pushdown Automata”).

• Konsep Terkait: Context-Free Grammars (CFG). PDA adalah mesin pengenal untuk Context-Free Languages (CFL), yaitu bahasa yang dapat dibangkitkan oleh CFG. Ada teorema yang membuktikan bahwa CFG dan PDA adalah ekuivalen.