PPT PDA, Pt. 1

Bahasa Sebuah Pushdown Automata

Ekuivalensi Metode Penerimaan:

Final State vs. Empty Stack

IF2224 Teori Bahasa Formal dan Otomata

---

Dua Cara PDA Menerima Bahasa (1)

Sebuah PDA dapat menerima sebuah string input dengan dua cara yang ekuivalen:

1. Acceptance by Final State ($L(P)$)

   • PDA selesai membaca seluruh input, dan berakhir di salah satu accepting state (anggota $F$).
   • Isi stack pada akhirnya tidak penting.

---

Dua Cara PDA Menerima Bahasa (1)

2. Acceptance by Empty Stack ($N(P)$)

   • PDA selesai membaca seluruh input, dan kondisi stack-nya benar-benar kosong ($ϵ$).
   • State akhir PDA pada akhirnya tidak penting.

---

Kedua metode ini sama kuatnya (ekuivalen). Kita dapat membuktikan ini dengan menunjukkan cara mengonstruksi satu jenis PDA dari jenis lainnya.

---

Bukti 1: Konversi Empty Stack $\to$ Final State (Diagram 6.4)

Tujuan: Mengubah PDA $P_N$ (yang menerima via empty stack) menjadi $P_F$ (yang menerima via final state).

Ide: Kita akan membuat PDA baru $P_F$ yang mensimulasikan $P_N$. $P_F$ akan menambahkan “penanda dasar” $X_0$ di stack. Jika $P_N$ berhasil mengosongkan stack-nya, $P_F$ akan “melihat” $X_0$ dan segera pindah ke final state baru, $p_f$.

---

Diagram 6.4 (Konstruksi $P_F$):

---

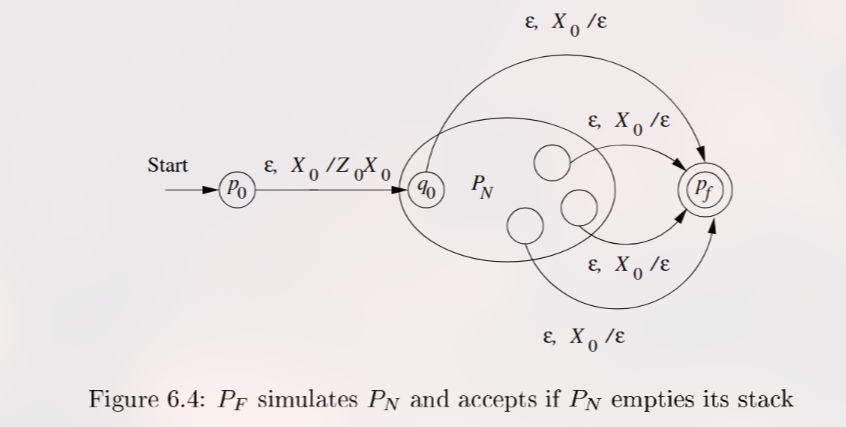
Penjelasan Diagram 6.4 (Peran State & Transisi)

Peran dan Fungsi State:

• p0 (New Start State):

  • Ini adalah start state baru untuk $P_F$.

  • Fungsinya hanya satu: melakukan inisialisasi. Ia meletakkan “penanda dasar” $X_0$ di stack, lalu meletakkan simbol start $Z_0$ milik $P_N$ di atasnya, dan kemudian menyerahkan kontrol ke start state lama, $q_0$.

---

• q0 (Old Start State):

  • Ini adalah start state dari $P_N$ (PDA lama). Simulasi $P_N$ dimulai dari sini.

---

• PN (Blok Simulasi):

  • Ini merepresentasikan semua state dan transisi orisinal dari $P_N$. $P_F$ menyalin dan menjalankan semua logika $P_N$ persis seperti aslinya.

---

• pf (New Final State):

  • Ini adalah satu-satunya final state di $P_F$.

  • $P_F$ hanya akan masuk ke state ini jika dan hanya jika $P_N$ (yang disimulasikan) telah mengosongkan stack aslinya.

---

Arti Transisi Kunci:

• $ϵ,X_0/Z_0{X}_0$ (dari $p_0$ ke $q_0$):

  • Tanpa membaca input ($ϵ$), jika top stack adalah $X_0$ (simbol start baru), ganti dengan $Z_0{X}_0$.

  • Artinya: PUSH simbol start lama ($Z_0$) di atas penanda dasar baru ($X_0$).

---

Arti Transisi Kunci:

• $ϵ,X_0/ϵ$ (dari semua state $P_N$ ke $p_f$):

  • Tanpa membaca input ($ϵ$), jika top stack adalah $X_0$, POP $X_0$ (ganti dengan $ϵ$).

  • Artinya: “Deteksi penanda dasar”. Ini adalah transisi yang memicu penerimaan.

---

Penjelasan Diagram 6.4 (Logika Penerimaan)

Bagaimana $P_F$ tahu $P_N$ telah mengosongkan stack?

---

$P_F$ tahu karena “penanda dasar” $X_0$ yang sebelumnya diletakkan di dasar stack, kini muncul di top stack. Ini hanya bisa terjadi jika $P_N$ (yang disimulasikan) telah berhasil mem-POP semua simbol di atasnya (termasuk $Z_0$ aslinya). Kemunculan $X_0$ adalah sinyal bahwa $P_N$ telah mencapai kondisi empty stack.

---

Mengapa acceptance via $P_f$, bukan empty stack?

---

Karena tujuan dari konstruksi ini adalah mengubah metode penerimaan. PDA lama ($P_N$) menerima dengan empty stack. PDA baru ($P_F$) harus menerima dengan final state. Kita “mendeteksi” kondisi empty stack $P_N$ (via $X_0$) dan “menerjemahkannya” menjadi kondisi final state $P_F$ (via transisi ke $p_f$).

---

Bagaimana $P_F$ memastikan sisa stack ($X_0$) bisa dihapus?

---

Transisi $ϵ,X_0/ϵ$ itulah yang melakukannya. Transisi ini tidak hanya memindahkan $P_F$ ke final state $p_f$, tetapi juga sekaligus mem-POP $X_0$ dari stack. Setelah $P_F$ berada di $p_f$, isi stack-nya menjadi $ϵ$ (kosong). Namun, ini tidak masalah, karena $P_F$ sudah berada di final state, dan definisi acceptance by final state tidak memedulikan isi stack akhir.

---

Trace Komputasi (Diagram 6.4)

• Contoh $P_N$ (Empty Stack): $L=\{i^n{e}^{n+1}\}$ (Contoh dari materi).

---

• Transisi $P_N$:

  • ${\delta }_N(q,i,Z)=(q,ZZ)$

  • ${\delta }_N(q,e,Z)=(q,ϵ)$

---

• Transisi $P_F$ (Baru):

  1. ${\delta }_F(p_0,ϵ,X_0)=(q,Z{X}_0)$

  2. ${\delta }_F(q,i,Z)=(q,ZZ)$ (Salinan)

  3. ${\delta }_F(q,e,Z)=(q,ϵ)$ (Salinan)

  4. ${\delta }_F(q,ϵ,X_0)=(p_f,ϵ)$ (Baru)

---

• Trace Input: “iee”

Step	Input	State	Stack	Transisi yang Digunakan
1	iee	p0	X0	(Inisialisasi)
2	iee	q	ZX0	(1) p0 $\to$ q, Push Z
3	ee	q	ZZX0	(2) Baca i, Push Z
4	e	q	ZX0	(3) Baca e, Pop Z
5	$ϵ$	q	X0	(3) Baca e, Pop Z
6	$ϵ$	pf	$ϵ$	(4) $ϵ$-move, Deteksi X0, Pop X0

---

Hasil: Input habis ($ϵ$), $P_F$ berakhir di state pf (sebuah final state).

Kesimpulan: String “iee” DITERIMA oleh $P_F$.

---

Bukti 2: Konversi Final State $\to$ Empty Stack (Diagram 6.7)

Tujuan: Mengubah PDA $P_F$ (yang menerima via final state) menjadi $P_N$ (yang menerima via empty stack).

Ide: Kita akan membuat $P_N$ baru yang mensimulasikan $P_F$. Jika $P_F$ masuk ke final state, $P_N$ akan memiliki transisi spontan untuk pindah ke state baru (“drain state” $p$). Tugas state $p$ ini hanya satu: mengosongkan sisa isi stack secepat mungkin.

Diagram 6.7 (Konstruksi $P_N$):

---

Slide 8: Penjelasan Diagram 6.7 (Peran State & Transisi)

Peran dan Fungsi State:

• p (Drain State):

  • Ini adalah state baru yang krusial untuk $P_N$.

  • Perannya adalah sebagai “mode kuras” (drain mode).

  • Begitu $P_N$ masuk ke state p, ia akan secara spontan (via $ϵ$-move) mem-POP simbol apapun dari stack, dan tetap berada di state p untuk melakukannya lagi, sampai stack benar-benar kosong.

Arti Transisi Kunci:

• $ϵ,X_0/Z_0{X}_0$ (dari $p_0$ ke $q_0$):

  • Sama seperti sebelumnya. Transisi inisialisasi untuk PUSH penanda dasar $X_0$ dan simbol start lama $Z_0$.

• $ϵ,\text{any}/ϵ$ (dari $F$ ke $p$, dan loop di $p$):

  • any berarti “simbol stack apapun” (semua $Y\in \Gamma \cup \{X_0\}$).

  • Artinya: “Tanpa membaca input ($ϵ$), apapun simbol di top stack, POP simbol itu.”

  • Transisi dari $F$ ke $p$ “mengaktifkan” mode kuras.

  • Transisi loop di $p$ “melanjutkan” mode kuras sampai stack habis.

---

Penjelasan Diagram 6.7 (Logika Penerimaan)

Kapan $P_N$ (baru) mengetahui $P_F$ (lama) sedang berada di final state?

$P_N$ mengetahuinya karena transisi spontan ($\epsilon, \text{any} / \epsilon$) dari final state (anggota $F$) ke drain state p menjadi “tersedia” atau “aktif”.

Karena PDA ini bersifat non-deterministik, jika $P_N$ (yang baru) berada di sebuah state $q$ yang merupakan final state di $P_F$ (lama), dan input telah habis, $P_N$ kini memiliki pilihan:

1. (Jika ada) Mengambil transisi $P_F$ lainnya.

2. Mengambil transisi spontan $\epsilon, \text{any} / \epsilon$ untuk pindah ke state p.

Jika input sudah habis, $P_N$ akan mengambil pilihan (2). Perpindahan ke state p ini memicu “mode kuras” yang akan menghabiskan sisa stack (termasuk $X_0$). Ketika stack akhirnya kosong, string DITERIMA oleh $P_N$ (sesuai definisi acceptance by empty stack).

---

Trace Komputasi (Diagram 6.7)

• Contoh $P_F$ (Final State): $L=\{w{w}^R\}$ (Misal $L_{wwr}$ dari materi).

• Transisi $P_F$ (disederhanakan):

  • (A) ${\delta }_F(q_0,0,Z_0)=(q_0,0Z_0)$ (Push)

  • (B) ${\delta }_F(q_0,ϵ,0)=(q_1,0)$ (Tebak tengah)

  • (C) ${\delta }_F(q_1,0,0)=(q_1,ϵ)$ (Pop)

  • (D) ${\delta }_F(q_1,ϵ,Z_0)=(q_2,Z_0)$ (Ke Final State $q_2$)

• Transisi $P_N$ (Baru):

  1. ${\delta }_N(p_0,ϵ,X_0)=(q_0,Z_0{X}_0)$

  2. Semua transisi $P_F$ (A, B, C, D) disalin.

  3. ${\delta }_N(q_2,ϵ,Y)=(p,ϵ)$ (Deteksi $F=\{q_2\}$, $Y\in \{0,1,Z_0,X_0\}$)

  4. ${\delta }_N(p,ϵ,Y)=(p,ϵ)$ (Loop kuras, $Y\in \{0,1,Z_0,X0\})$

• Trace Input: “00”

Step	Input	State	Stack	Transisi yang Digunakan
1	00	p0	X0	(Inisialisasi)
2	00	q0	Z0X0	(1) p0 \rightarrow q0, Push Z0
3	0	q0	0Z0X0	(A) Baca 0, Push 0
4	0	q1	0Z0X0	(B) $ϵ$-move, tebak tengah
5	$ϵ$	q1	Z0X0	(C) Baca 0, Pop 0
6	$ϵ$	q2	Z0X0	(D) $ϵ$-move, ke final state q2
7	$ϵ$	p	X0	(3) $ϵ$-move, deteksi q2, Pop Z0
8	$ϵ$	p	$ϵ$	(4) $ϵ$-move, loop kuras, Pop X0

Hasil: Input habis ($ϵ$), Stack akhir ($ϵ$).

Kesimpulan: String “00” DITERIMA oleh $P_N$.

---

Kesimpulan

• Kita telah membuktikan bahwa kedua metode penerimaan PDA adalah ekuivalen.

• $N(P)\to L(P)$: Setiap PDA empty stack dapat diubah menjadi PDA final state dengan menambahkan penanda dasar stack ($X_0$) dan final state baru ($p_f$) untuk mendeteksi penanda tersebut.

• $L(P)\to N(P)$: Setiap PDA final state dapat diubah menjadi PDA empty stack dengan menambahkan “drain state” ($p$) yang akan mengosongkan stack secara otomatis ketika final state (lama) tercapai.

• Artinya, kekuatan komputasi kedua model adalah sama.