Prinsip dan Algoritma Desain DFA

Back to IF2224 Teori Bahasa Formal dan Otomata

Topic

Questions/Cues

• Apa filosofi dasar desain DFA?
• Apa 3 syarat utama sebuah state?
• Bagaimana algoritma desainnya?
• Apa arti dari setiap state?
• Studi Kasus: Genap 0 & Genap 1?
• Bagaimana menangani operasi “or” / “not”?

Reference Points

• 2022_catatan-kuliah-Algoritma-membuat-DFA.pdf
• 2019_How to Design a DFA.pptx

Filosofi Utama: State adalah Memori

Kunci utama dalam merancang sebuah DFA adalah memahami bahwa setiap state mewakili sebuah “ingatan” atau kondisi spesifik dari string yang telah dibaca sejauh ini. DFA tidak memiliki memori eksternal, jadi satu-satunya cara ia bisa “mengingat” informasi penting (misalnya, “apakah jumlah 0 sejauh ini genap?” atau “apakah simbol terakhir yang dibaca adalah 1?”) adalah dengan berada di state yang berbeda.

Setiap state harus memiliki arti atau interpretasi yang jelas dan bisa dideskripsikan.

Syarat-Syarat State dalam DFA

Saat mendefinisikan state, ada tiga aturan utama yang harus dipatuhi:

1. Keadaan Diterima Harus Menjadi State: Kondisi apa pun yang menyebabkan sebuah string diterima (menjadi bagian dari bahasa) harus bisa diwakili sebagai sebuah state (atau beberapa state).
2. Keadaan State Tidak Boleh Beririsan: Makna dari satu state tidak boleh tumpang tindih dengan makna state lain. Misalnya, mendefinisikan $q_0$​ sebagai “jumlah ‘0’ genap” dan $q_1$​ sebagai “jumlah ‘1’ genap” adalah salah, karena string “0011” memenuhi kedua kondisi tersebut. Seharusnya, satu state merepresentasikan kombinasi kondisi yang unik.
3. Semua Kemungkinan Keadaan Harus Terakomodasi: Seluruh kemungkinan kondisi yang relevan dengan permasalahan bahasa harus terwakili oleh salah satu state yang ada. Tidak boleh ada kondisi yang terlewat.

Algoritma Desain DFA

Berikut adalah proses sistematis untuk merancang DFA:

• Buat Test Set: Tuliskan beberapa contoh string yang seharusnya diterima dan beberapa contoh yang seharusnya ditolak. Ini akan sangat membantu untuk menguji DFA kita nanti.
• Definisikan Semua State: Identifikasi semua kemungkinan kondisi/keadaan yang perlu diingat oleh mesin. Pastikan kondisi-kondisi ini tidak beririsan dan mencakup semua kemungkinan. Beri nama dan deskripsi yang jelas untuk setiap state.
• Gambarkan Transisi: Untuk setiap state, tentukan ke mana mesin akan berpindah jika menerima setiap simbol dari alphabet. Transisi ini harus konsisten dengan arti dari masing-masing state.
• Tentukan Start dan Final State:
  • Start State: Biasanya merepresentasikan kondisi awal sebelum membaca string apa pun (misalnya, kondisi saat baru membaca string kosong, ϵ).
  • Final State: Pilih state (atau beberapa state) yang definisinya cocok dengan kriteria string yang diterima oleh bahasa.
• Uji dengan Test Set: Gunakan string dari langkah 1 untuk menelusuri DFA yang telah dibuat dan pastikan hasilnya sesuai (diterima atau ditolak).

Studi Kasus: DFA untuk String dengan Jumlah ‘0’ Genap dan Jumlah ‘1’ Genap

Misalkan $L=\{w|w$ memiliki jumlah ’0’ genap DAN jumlah ’1’ genap$\}$.

1. Definisi State: Kita butuh 4 kondisi untuk melacak paritas (genap/ganjil) dari ‘0’ dan ‘1’.
   • $q_0$: Jumlah ‘0’ genap, jumlah ‘1’ genap.
   • $q_1$: Jumlah ‘0’ genap, jumlah ‘1’ ganjil.
   • $q_2$: Jumlah ‘0’ ganjil, jumlah ‘1’ genap.
   • $q_3$: Jumlah ‘0’ ganjil, jumlah ‘1’ ganjil.
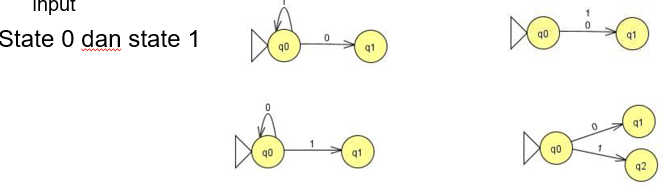
2. Transisi:
   • Dari $q_0$​ (genap, genap): jika baca ‘0’ → $q_2$​ (ganjil, genap). Jika baca ‘1’ → $q_1$ (genap, ganjil).
   • Dari $q_1$ (genap, ganjil): jika baca ‘0’ → $q_3$ (ganjil, ganjil). Jika baca ‘1’ → $q_0$ (genap, genap).
   • Dari $q_2$ (ganjil, genap): jika baca ‘0’ → $q_0$ (genap, genap). Jika baca ‘1’ → $q_3$ (ganjil, ganjil).
   • Dari $q_3$ (ganjil, ganjil): jika baca ‘0’ → $q_1$​ (genap, ganjil). Jika baca ‘1’ → $q_2$ (ganjil, genap).
3. Start & Final State:
   • Start State: Kondisi awal (string kosong) memiliki nol buah ‘0’ dan nol buah ‘1’ (keduanya genap). Jadi, start state adalah q0​.
   • Final State: Bahasa ini menerima string dengan ‘0’ genap dan ‘1’ genap. Kondisi ini persis seperti definisi state q0​. Jadi, final state adalah q0​.

Aturan Khusus untuk Operasi Bahasa

Terkadang, bahasa didefinisikan sebagai kombinasi dari bahasa lain. Berikut panduan singkatnya:

• Jika Bahasa mengandung “OR” (atau): Buat DFA untuk masing-masing sub-bahasa, lalu gabungkan dengan membuat “cabang” dari start state. (Catatan: Ini menyederhanakan konsep, biasanya menghasilkan NFA yang perlu diubah lagi).
• Jika Bahasa mengandung “NOT” (bukan): Buat DFA untuk bahasa positifnya (tanpa “not”). Lalu, ubah semua final state menjadi non-final, dan semua non-final state menjadi final. Ini disebut operasi komplemen.
• Jika Bahasa mengandung “AND” (dan): Buat DFA untuk masing-masing sub-bahasa. (Catatan: Penggabungannya lebih kompleks, biasanya menggunakan metode product construction, bukan sekadar konkatenasi).

Summary

Mendesain sebuah DFA adalah proses sistematis yang berpusat pada filosofi bahwa setiap state adalah sebuah memori yang merepresentasikan kondisi unik dan tidak tumpang tindih dari string yang telah dibaca. Prosesnya meliputi pendefinisian semua state yang diperlukan, menentukan transisi yang logis antar state berdasarkan input, menetapkan state awal dan akhir sesuai kondisi bahasa, dan terakhir mengujinya. Dengan memahami bahwa arti dari setiap state adalah kunci, perancangan DFA yang kompleks sekalipun dapat dipecah menjadi langkah-langkah yang dapat dikelola.

Additional Information (Optional)

Pola Desain Umum: Trap State (State Jebakan)

Saat merancang DFA, Anda akan sering menemukan kebutuhan akan trap state. Ini adalah state non-final yang, sekali dimasuki, tidak akan pernah bisa keluar. Semua transisi dari trap state akan kembali ke dirinya sendiri. Gunanya adalah untuk “membuang” semua string yang sudah dipastikan melanggar aturan bahasa. Misalnya, pada DFA yang menolak “11”, state C adalah sebuah trap state. Begitu mesin membaca “11”, ia masuk ke C dan akan tetap di sana selamanya, memastikan string tersebut ditolak.

Eksplorasi Mandiri

• Tantangan Desain: Coba rancang DFA untuk bahasa L={w∣w adalah string biner yang mengandung substring ’01’}.
• Petunjuk: Pikirkan kondisi-kondisi memori yang Anda perlukan. Anda mungkin butuh state-state dengan arti sebagai berikut:
  1. “Belum melihat ‘0’ ataupun ‘01’” (Ini bisa jadi start state).
  2. “Baru saja melihat ‘0’, tapi belum melihat ‘01’“.
  3. “Sudah pernah melihat substring ‘01’” (Ini pasti final state, dan mungkin sebuah trap state yang menerima).