Decision Tree Learning (DTL) (ID3)

Back to IF3170 Inteligensi Artifisial

Topic
Questions/Cues

Apa saja tipe-tipe atribut data?

Apa itu DTL (Decision Tree Learning)?

Bagaimana representasi DTL?

Kenapa & Kapan kita menggunakan DTL?

Apa itu Algoritma ID3?

Bagaimana alur kerja ID3?

Kapan algoritma DTL berhenti?

Apa itu ‘Best Attribute’?

Apa itu Entropy?

Apa arti nilai Entropy (0 vs 1)?

Apa itu Information Gain?

Bagaimana cara menghitung Gain?

Bagaimana contoh perhitungan (Play Tennis)?

Apa langkah selanjutnya setelah dapat root?

Reference Points

Slides 19. IF3170_DTL.pdf

Source: Machine Learning, Tom Mitchell

Source: DataMining Concepts and Techniques by Jiawei Han, et al.
Bagian 1: Tipe-Tipe Atribut Data

Sebelum membangun model, kita harus paham data kita. Atribut (fitur) data umumnya dibagi menjadi:

Numeric (Quantitative): Berupa angka yang bisa diukur.

Interval-Scaled: Angka yang punya urutan dan unit yang sama (misal: Temperatur, Tanggal). Kita bisa hitung selisihnya, tapi “0” tidak berarti “tidak ada”.

Ratio-Scaled: Seperti interval, tapi punya titik “nol” yang absolut (misal: Berat, Umur, Gaji). Kita bisa bilang “20kg adalah dua kali lipat 10kg”.

Categorical (Qualitative):

Nominal: Simbol atau nama (misal: Occupation Type, Zip Code, Student_ID). Angka di sini (spt Zip Code) tidak bisa dioperasikan secara matematis.

Binary: Hanya punya 2 state (misal: Gender, HIV Positive/Negative).

Symmetric: Kedua state sama pentingnya (misal: Laki-laki/Perempuan).

Asymmetric: Satu state lebih penting/langka (misal: HIV Positive lebih penting daripada Negative).

Ordinal: Punya urutan atau ranking yang bermakna, tapi jarak antar nilai tidak diketahui (misal: Drink Size (Small, Medium, Large), Grades (A, B, C), Customer Satisfaction (1-5)).

Bagian 2: Apa, Kenapa, dan Kapan DTL

Apa itu DTL (Decision Tree Learning)?

DTL adalah salah satu metode Supervised Learning untuk mengaproksimasi (memperkirakan) sebuah fungsi target yang bernilai diskrit.

Model yang dihasilkannya disebut Decision Tree (Pohon Keputusan). Pohon ini juga bisa dengan mudah diubah menjadi satu set aturan IF-THEN.

Representasi DTL

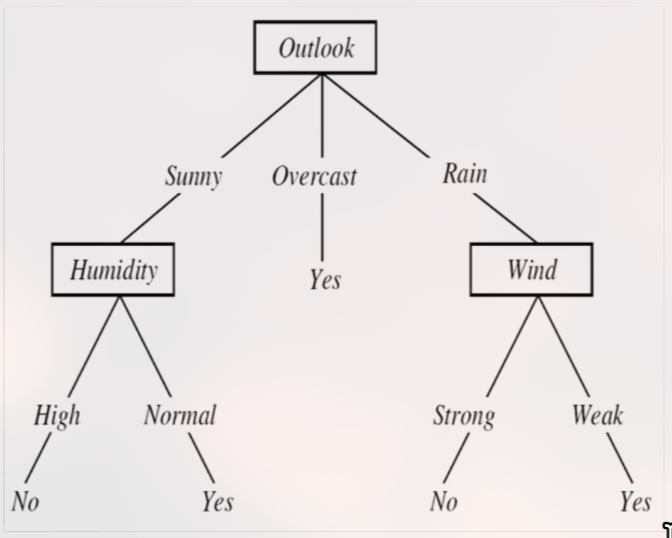
Sebuah Decision Tree terdiri dari:

Internal Node (Simpul Internal): Merepresentasikan sebuah tes pada satu atribut (misal: tes atribut Outlook).

Branch (Cabang): Merepresentasikan salah satu nilai dari atribut tersebut (misal: cabang Sunny, Overcast, Rain).

Leaf Node (Simpul Daun): Merepresentasikan hasil klasifikasi (misal: Play Tennis = Yes).

Sebuah path dari root ke leaf merepresentasikan sebuah aturan konjungsi (AND). Keseluruhan pohon merepresentasikan disjunction of conjunctions (OR dari aturan-aturan AND).

Contoh: (Outlook=Sunny AND Humidity=Normal) OR (Outlook=Overcast) OR …

Kenapa Menggunakan DTL?

Mudah Dipahami: Hasil pohonnya sangat intuitif dan mudah dijelaskan (interpretability tinggi).

Robust terhadap Noisy Data: Cukup tahan terhadap data yang error.

Mampu Mempelajari Ekspresi Disjunctive: Bisa menangani logika (A AND B) OR (C AND D).

Kapan Menggunakan DTL?

DTL sangat cocok untuk masalah di mana:

Instans/data direpresentasikan sebagai pasangan atribut-nilai.

Target Function (Kelas) memiliki nilai diskrit (misal: Yes/No, Kucing/Anjing).

Data latih mungkin mengandung errors (noise) atau missing attribute values.

Bagian 3: Algoritma Dasar (ID3)

Apa itu Algoritma ID3?

ID3 (Iterative Dichotomiser 3) adalah algoritma DTL klasik yang membangun pohon menggunakan pendekatan Top-Down dan Greedy Search.

Top-Down: Membangun pohon dari root (atas) ke leaf (bawah).

Greedy: Di setiap langkah, ia memilih keputusan terbaik saat itu juga (optimum lokal) tanpa memikirkan apakah keputusan itu akan optimal secara global.

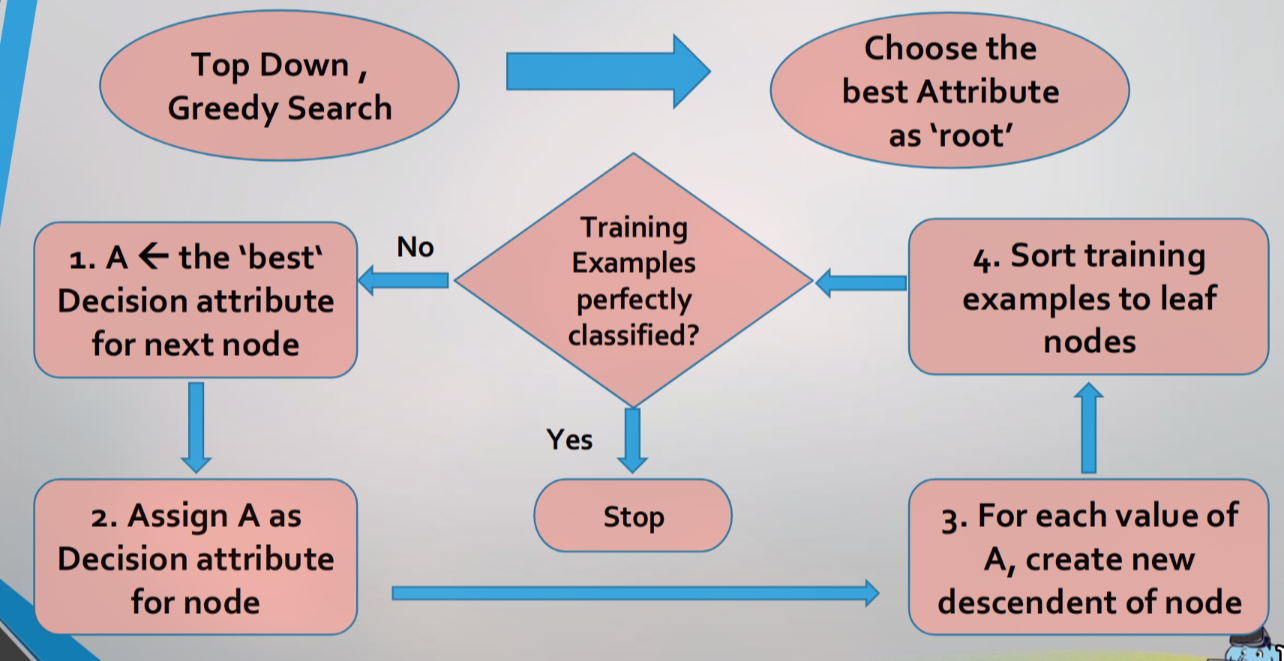
Alur Kerja ID3

Mulai dari root node.

Pilih “best attribute” (atribut terbaik) untuk memecah data. (Kita akan bahas cara memilihnya di Bagian 4).

Jadikan atribut tersebut sebagai node keputusan.

Buat cabang (branch) baru untuk setiap nilai dari atribut tersebut.

Bagi (sortir) data latih ke cabang-cabang yang sesuai.

Ulangi proses ini (rekursif) untuk setiap cabang (yang sekarang menjadi subset data) sampai stopping condition terpenuhi.

Kapan ID3 Berhenti (Stopping Condition)?

Sebuah cabang akan berhenti dan menjadi leaf node jika:

Semua contoh di cabang itu memiliki kelas yang sama (misal: semua ‘Yes’). Ini disebut pure node.

Tidak ada atribut lagi yang bisa digunakan untuk memecah data. Jika ini terjadi, leaf node mengambil kelas mayoritas dari data di cabang itu (disebut PLURALITY-VALUE).

Tidak ada contoh data di cabang itu. Jika ini terjadi, leaf node mengambil kelas mayoritas dari parent-nya.

Bagian 4: Matematika Inti (Entropy & Information Gain)

Bagaimana ID3 Memilih “Best Attribute”?

ID3 memilih atribut yang paling efektif memisahkan data menjadi subset-subset yang pure (murni satu kelas). Ukuran untuk ini disebut Information Gain.

Untuk menghitung Information Gain, kita harus paham Entropy terlebih dahulu.

Apa itu Entropy?

Entropy adalah ukuran ketidakpastian (uncertainty), keacakan (randomness), atau impurity (ketidakmurnian) dari sebuah set data S.

$E n t ro p y (S) \equiv \sum_{i = 1}^{c} - p_{i} lo g_{2} p_{i}$

c = jumlah kelas (misal: 2, untuk Yes/No).

p_i = proporsi contoh yang termasuk kelas i.

Arti Nilai Entropy (untuk 2 kelas):

Entropy = 0: Set pure (murni). p_i = 1 atau p_i = 0. (Misal: 4 Yes, 0 No). Tidak ada ketidakpastian, kita sudah tahu pasti hasilnya.

Entropy = 1: Set impure maksimal. p_i = 0.5. (Misal: 5 Yes, 5 No). Ketidakpastian maksimal, seperti melempar koin.

Apa itu Information Gain?

Information Gain adalah ukuran pengurangan Entropy yang kita dapatkan setelah memecah set data S menggunakan sebuah atribut A.

$G ain (S, A) \equiv E n t ro p y (S) - \sum_{v \in Va l u es (A)} \frac{∣ S _{v} ∣}{∣ S ∣} E n t ro p y (S_{v})$

Entropy(S): Entropy sebelum dipecah (entropy parent).

Values(A): Nilai-nilai yang dimiliki atribut A (misal: Sunny, Overcast, Rain).

|S_v| / |S|: Proporsi data yang memiliki nilai v (ini adalah “bobot”).

Entropy(S_v): Entropy dari subset data setelah dipecah (entropy anak).

Sederhananya: Gain = Entropy(Parent) - Rata-rata_Tertimbang_Entropy(Anak).

Contoh Perhitungan (Play Tennis, hal 23-25)

Hitung Entropy Awal (Parent S):

Data S: 14 hari. [9 ‘Yes’, 5 ‘No’].

Entropy(S) = -(9/14)log₂(9/14) - (5/14)log₂(5/14) = 0.940

Hitung Gain untuk Atribut Outlook:

Outlook=Sunny: [2 Yes, 3 No]. Entropy(S_sunny) = 0.971

Outlook=Overcast: [4 Yes, 0 No]. Entropy(S_overcast) = 0 (Pure!)

Outlook=Rain: [3 Yes, 2 No]. Entropy(S_rain) = 0.971

Gain(S, Outlook) = 0.940 - [ (5/14) * 0.971 + (4/14) * 0 + (5/14) * 0.971 ]

Gain(S, Outlook) = 0.940 - [ 0.347 + 0 + 0.347 ] = 0.246

Hitung Gain untuk Atribut Humidity:

Humidity=High: [3 Yes, 4 No]. Entropy(S_high) = 0.985

Humidity=Normal: [6 Yes, 1 No]. Entropy(S_normal) = 0.592

Gain(S, Humidity) = 0.940 - [ (7/14) * 0.985 + (7/14) * 0.592 ]

Gain(S, Humidity) = 0.940 - [ 0.493 + 0.296 ] = 0.151

Bandingkan (hal 25):

Gain(S, Outlook) = 0.246 (Tertinggi)

Gain(S, Humidity) = 0.151

Gain(S, Wind) = 0.048

Gain(S, Temperature) = 0.029

Keputusan: Karena Gain(S, Outlook) adalah yang terbesar, algoritma ID3 memilih Outlook sebagai root node.

Langkah Selanjutnya (Rekursif, hal 26)

Cabang Overcast menjadi leaf node ‘Yes’ (karena Entropy=0).

Untuk cabang Sunny, kita ambil subset datanya [D1, D2, D8, D9, D11] dan ulangi proses: hitung Gain(S_sunny, Humidity), Gain(S_sunny, Temp), Gain(S_sunny, Wind). Di contoh ini, Humidity menang dan menjadi node di bawah Sunny.

Bagian 5: Latihan

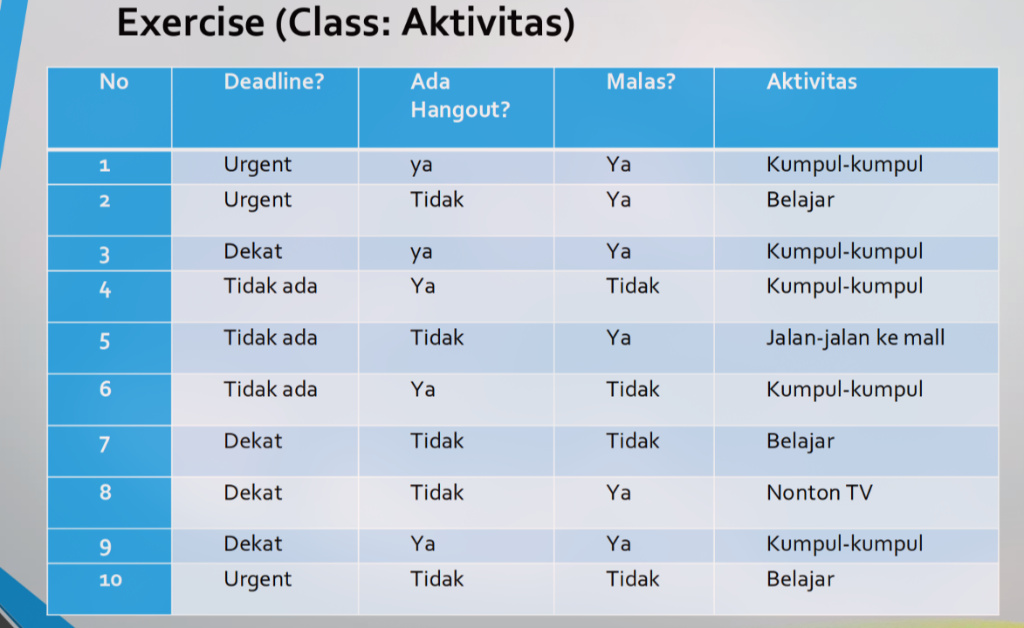
Data Latih (Set S): Total 10 instans Kelas Target (Aktivitas): 4 kelas

Kumpul-kumpul (K): 5 instans

Belajar (B): 3 instans

Jalan-jalan ke mall (J): 1 instans

Nonton TV (N): 1 instans

Atribut: Deadline?, Ada Hangout?, Malas?

Langkah 1: Hitung Entropy Awal (Parent S)

S memiliki 4 kelas [5 K, 3 B, 1 J, 1 N] dari total 10 data.

Entropy(S) = -[ p(K)log₂(p(K)) + p(B)log₂(p(B)) + p(J)log₂(p(J)) + p(N)log₂(p(N)) ] Entropy(S) = -[ (5/10)log₂(5/10) + (3/10)log₂(3/10) + (1/10)log₂(1/10) + (1/10)log₂(1/10) ] Entropy(S) = -[ (0.5 * -1) + (0.3 * -1.737) + (0.1 * -3.322) + (0.1 * -3.322) ] Entropy(S) = -[ -0.5 - 0.5211 - 0.3322 - 0.3322 ] Entropy(S) = -[ -1.6855 ] = 1.6855

Langkah 2: Hitung Information Gain untuk Setiap Atribut

A. Gain(S, Deadline?)

Deadline? = Urgent (3 data): [1 K, 2 B] E(S_Urgent) = -[ (1/3)log₂(1/3) + (2/3)log₂(2/3) ] = 0.918

Deadline? = Dekat (4 data): [2 K, 1 B, 1 N] E(S_Dekat) = -[ (2/4)log₂(2/4) + (1/4)log₂(1/4) + (1/4)log₂(1/4) ] = 1.5

Deadline? = Tidak ada (3 data): [2 K, 1 J] E(S_TidakAda) = -[ (2/3)log₂(2/3) + (1/3)log₂(1/3) ] = 0.918

Gain(S, Deadline) = E(S) - [ (3/10)*E(S_Urgent) + (4/10)*E(S_Dekat) + (3/10)*E(S_TidakAda) ] Gain(S, Deadline) = 1.6855 - [ (0.3 * 0.918) + (0.4 * 1.5) + (0.3 * 0.918) ] Gain(S, Deadline) = 1.6855 - [ 0.2754 + 0.6 + 0.2754 ] = 1.6855 - 1.1508 = 0.5347

B. Gain(S, Ada Hangout?)

Ada Hangout? = ya (5 data): [5 K] E(S_ya) = 0 (Pure!)

Ada Hangout? = Tidak (5 data): [3 B, 1 J, 1 N] E(S_Tidak) = -[ (3/5)log₂(3/5) + (1/5)log₂(1/5) + (1/5)log₂(1/5) ] = 1.371

Gain(S, Hangout) = E(S) - [ (5/10)*E(S_ya) + (5/10)*E(S_Tidak) ] Gain(S, Hangout) = 1.6855 - [ (0.5 * 0) + (0.5 * 1.371) ] Gain(S, Hangout) = 1.6855 - 0.6855 = 1.0

C. Gain(S, Malas?)

Malas? = Ya (6 data): [3 K, 1 B, 1 J, 1 N] E(S_Ya) = -[ (3/6)log₂(3/6) + (1/6)log₂(1/6) + (1/6)log₂(1/6) + (1/6)log₂(1/6) ] = 1.793

Malas? = Tidak (4 data): [2 K, 2 B] E(S_Tidak) = -[ (2/4)log₂(2/4) + (2/4)log₂(2/4) ] = 1.0

Gain(S, Malas) = E(S) - [ (6/10)*E(S_Ya) + (4/10)*E(S_Tidak) ] Gain(S, Malas) = 1.6855 - [ (0.6 * 1.793) + (0.4 * 1.0) ] Gain(S, Malas) = 1.6855 - [ 1.0758 + 0.4 ] = 1.6855 - 1.4758 = 0.2097

Langkah 3: Bandingkan Gain & Tentukan Root Node

Gain(S, Ada Hangout?) = 1.0 (Tertinggi)

Gain(S, Deadline?) = 0.5347

Gain(S, Malas?) = 0.2097

Kesimpulan: Atribut Ada Hangout? dipilih sebagai root node karena memiliki Information Gain tertinggi.

Cabang Ada Hangout? = ya akan langsung menjadi leaf node “Kumpul-kumpul” (karena datanya sudah pure).

Cabang Ada Hangout? = Tidak perlu dipecah lebih lanjut menggunakan sisa atribut (Deadline? dan Malas?).

Langkah 4: Proses Detail untuk Branch Ada Hangout? = Tidak

Filter Dataset: Kita sekarang hanya peduli pada data di mana Ada Hangout? = Tidak. Dari 10 data awal, kita mendapatkan subset baru (S_tidak) yang berisi 5 data:

No Deadline? Ada Hangout? Malas? Aktivitas
2 Urgent Tidak Ya Belajar
5 Tidak ada Tidak Ya Jalan-jalan ke mall
7 Dekat Tidak Tidak Belajar
8 Dekat Tidak Ya Nonton TV
10 Urgent Tidak Tidak Belajar

Analisis Subset Baru

Atribut Tersisa: Kita tidak bisa lagi menggunakan Ada Hangout? (karena semua nilainya sama). Atribut yang tersisa untuk diuji adalah: Deadline? dan Malas?.

Kelas Tersisa: Kelas ‘Kumpul-kumpul’ sudah tidak ada di subset ini. Kelas yang kita miliki sekarang adalah [3 Belajar, 1 Jalan-jalan ke mall, 1 Nonton TV].

Subset ini Impure (tidak murni), jadi kita harus memecahnya lagi.

Langkah Perhitungan (Hitung Ulang Gain)

Kita ulangi proses ID3, tapi hanya pada subset 5 data ini:

Hitung Entropy Parent Baru: Hitung Entropy(S_tidak): E(S_tidak) = -[ (3/5)log₂(3/5) + (1/5)log₂(1/5) + (1/5)log₂(1/5) ] = 1.371

Hitung Gain (Baru) untuk Atribut Tersisa:

Gain(S_tidak, Deadline?)

Urgent (2 data): [2 Belajar] → E = 0

Dekat (2 data): [1 Belajar, 1 Nonton TV] → E = 1.0

Tidak ada (1 data): [1 Jalan-jalan] → E = 0

Gain = 1.371 - [ (2/5)*0 + (2/5)*1.0 + (1/5)*0 ] = 1.371 - 0.4 = 0.971

Gain(S_tidak, Malas?)

Ya (3 data): [1 Belajar, 1 Jalan-jalan, 1 Nonton TV] → E = 1.585

Tidak (2 data): [2 Belajar] → E = 0

Gain = 1.371 - [ (3/5)*1.585 + (2/5)*0 ] = 1.371 - 0.951 = 0.42

Pilih Pemenang: Atribut dengan Gain tertinggi di antara Deadline? dan Malas? akan menjadi node berikutnya di bawah cabang Ada Hangout? = Tidak.

Gain(Deadline?) (0.971) > Gain(Malas?) (0.42).

Maka, node selanjutnya di bawah Ada Hangout? = Tidak adalah Deadline?.

Sekarang, node Deadline? itu sendiri punya 3 cabang (Urgent, Dekat, Tidak ada). Kita harus periksa satu per satu:

Cabang Deadline? = Urgent: E = 0 ⇒ Pure, langsung menjadi Leaf Node (Belajar)

Cabang Deadline? = Tidak ada: E = 0 ⇒ Pure, langsung menjadi Leaf Node (Jalan-jalan ke mall)

Cabang Deadline? = Dekat: E != 0 ⇒ Impure, branching lagi dengan atribut Malas (Bisa dihitung lebih lanjut).

Berikut adalah visualisasi branching lengkapnya:
graph TD
 E1("Ada Hangout?") -->|ya| k["Kumpul-kumpul"];
 E1 -->|Tidak| E2("Deadline?");
 
 E2 -->|Urgent| E3["Belajar"];
 E2 -->|Tidak ada| E4["Jalan-jalan ke mall"];
 E2 -->|Dekat| E5("Malas?");
 
 E5 -->|Tidak| E6["Belajar"];
 E5 -->|Ya| E7["Nonton TV"];
Bagian 5: Kelemahan DTL

DTL memiliki beberapa kelemahan:

Overfitting training data: Pohon bisa menjadi terlalu kompleks dan “menghafal” data latih, termasuk noise (error). Akibatnya, pohon tersebut bekerja sangat baik pada data latih tetapi sangat buruk pada data baru yang belum pernah dilihat. Solusinya adalah pruning (pemangkasan).

Continuous-valued Attribute (Atribut Bernilai Kontinu): Algoritma dasar seperti ID3 dirancang untuk atribut kategorikal (seperti ‘Sunny’, ‘Rain’). Ketika berhadapan dengan angka kontinu (seperti Temperatur = 25.5), algoritma harus melakukan pekerjaan ekstra untuk menemukan “titik potong” (split point) terbaik (misal, Temperatur < 30), yang bisa jadi mahal secara komputasi.

Handling missing attribute value (Menangani nilai atribut yang hilang): Data di dunia nyata seringkali tidak lengkap (ada nilai ‘Null’ atau ’?’). DTL harus punya strategi untuk menangani ini, misalnya dengan mengabaikan data tersebut, mengisinya dengan nilai mayoritas, atau memecah data secara fraksional saat menghitung Gain.

Alternative measures for selecting attributes (Ukuran alternatif untuk memilih atribut): Metrik standar Information Gain (yang digunakan ID3) memiliki bias: ia cenderung lebih menyukai atribut yang memiliki banyak nilai unik (seperti ‘StudentID’). Metrik alternatif seperti Gain Ratio (digunakan C4.5) atau Gini Impurity (digunakan CART) dibuat untuk mengatasi bias ini.

Handling attributes with differing costs (Menangani atribut dengan biaya berbeda): Dalam masalah nyata (misal, diagnosis medis), mendapatkan data untuk suatu atribut (seperti ‘Hasil MRI’) bisa jauh lebih mahal daripada atribut lain (seperti ‘Ukur Suhu Tubuh’). Algoritma standar tidak memperhitungkan “biaya” ini. Perlu modifikasi agar pohon lebih memilih atribut yang murah namun tetap informatif.

No	Deadline?	Ada Hangout?	Malas?	Aktivitas
2	Urgent	Tidak	Ya	Belajar
5	Tidak ada	Tidak	Ya	Jalan-jalan ke mall
7	Dekat	Tidak	Tidak	Belajar
8	Dekat	Tidak	Ya	Nonton TV
10	Urgent	Tidak	Tidak	Belajar

Summary

Decision Tree Learning (DTL) adalah algoritma Supervised Learning yang membangun model pohon keputusan secara Top-Down dan Greedy. Inti dari algoritmanya (seperti ID3) adalah memilih atribut terbaik di setiap langkah dengan cara menghitung Information Gain. Information Gain adalah metrik yang mengukur seberapa besar penurunan Entropy (ketidakpastian) setelah data dipecah berdasarkan atribut tersebut. Atribut dengan Gain tertinggi dipilih, dan proses ini diulangi secara rekursif hingga leaf node (hasil klasifikasi) tercapai.

Additional Information

Pendalaman 1: Masalah Terbesar ID3 - Overfitting

Karena sifatnya yang greedy dan tujuannya membuat pure node, DTL sangat rentan terhadap Overfitting. Artinya, pohon menjadi terlalu kompleks dan “menghafal” data latih (termasuk noise-nya), sehingga performanya buruk saat bertemu data baru.

Solusi (Pruning/Pemangkasan):

Pre-Pruning (Early Stopping): Menghentikan pertumbuhan pohon lebih awal (misal: jika Gain terlalu kecil, atau jumlah data di node terlalu sedikit).

Post-Pruning: Membuat pohon tumbuh sepenuhnya, lalu memangkas kembali cabang-cabang yang tidak signifikan (yang paling umum digunakan).

Pendalaman 2: Kelemahan Information Gain (Bias)

Metrik Information Gain memiliki bias atau kecenderungan untuk lebih menyukai atribut yang memiliki banyak nilai unik (high-cardinality), seperti StudentID atau Timestamp.

Kenapa? Atribut StudentID akan memecah data menjadi N cabang, di mana setiap cabang hanya berisi 1 data. Setiap cabang ini akan pure (Entropy=0), sehingga Gain-nya akan menjadi maksimal. Padahal, atribut ini sama sekali tidak berguna untuk generalisasi.

Solusi: Gunakan metrik Gain Ratio (digunakan oleh algoritma C4.5). Gain Ratio menormalisasi Information Gain dengan SplitInfo (entropy dari atribut itu sendiri), sehingga “menghukum” atribut yang memiliki banyak nilai.

Pendalaman 3: Menangani Atribut Numerik (Kontinu)

Algoritma ID3 dasar (seperti di PDF) hanya bekerja untuk atribut diskrit (kategorikal).

Bagaimana dengan Temperature atau Humidity jika angkanya kontinu (misal: 25.5, 30.1)?

Solusi (Discretization): Kita harus “mem-binarisasi” data. Algoritma harus mencari titik potong (split point) terbaik (misal: Temperature < 70 dan Temperature >= 70) yang akan menghasilkan Information Gain terbesar. Ini menambah kompleksitas komputasi.

Pendalaman 4: Dari ID3 ke Algoritma Modern

C4.5: Penerus ID3. Menggunakan Gain Ratio (mengatasi bias) dan bisa menangani atribut kontinu serta missing values.

CART: Algoritma lain yang membangun pohon biner (hanya 2 cabang per node) dan menggunakan metrik Gini Impurity.

Random Forest & Gradient Boosting: Ini adalah algoritma Ensemble. Alih-alih membangun 1 pohon yang “sempurna”, mereka membangun ratusan atau ribuan pohon “cukup baik” dan menggabungkan hasilnya (lewat voting atau averaging) untuk mendapatkan prediksi yang jauh lebih kuat dan tidak overfitting.

IF Notes

Explorer

Decision Tree Learning (DTL) (ID3)

Questions/Cues

Reference Points

Bagian 1: Tipe-Tipe Atribut Data

Bagian 2: Apa, Kenapa, dan Kapan DTL

Apa itu DTL (Decision Tree Learning)?

Representasi DTL

Kenapa Menggunakan DTL?

Kapan Menggunakan DTL?

Bagian 3: Algoritma Dasar (ID3)

Apa itu Algoritma ID3?

Alur Kerja ID3

Kapan ID3 Berhenti (Stopping Condition)?

Bagian 4: Matematika Inti (Entropy & Information Gain)

Bagaimana ID3 Memilih “Best Attribute”?

Apa itu Entropy?

Apa itu Information Gain?

Contoh Perhitungan (Play Tennis, hal 23-25)

Langkah Selanjutnya (Rekursif, hal 26)

Bagian 5: Latihan

Langkah 1: Hitung Entropy Awal (Parent `S`)

Langkah 2: Hitung Information Gain untuk Setiap Atribut

Langkah 3: Bandingkan Gain & Tentukan Root Node

Langkah 4: Proses Detail untuk Branch `Ada Hangout? = Tidak`

Bagian 5: Kelemahan DTL

Pendalaman 1: Masalah Terbesar ID3 - Overfitting

Pendalaman 2: Kelemahan Information Gain (Bias)

Pendalaman 3: Menangani Atribut Numerik (Kontinu)

Pendalaman 4: Dari ID3 ke Algoritma Modern

Graph View

Table of Contents

Backlinks

IF Notes

Explorer

Decision Tree Learning (DTL) (ID3)

Questions/Cues

Reference Points

Bagian 1: Tipe-Tipe Atribut Data

Bagian 2: Apa, Kenapa, dan Kapan DTL

Apa itu DTL (Decision Tree Learning)?

Representasi DTL

Kenapa Menggunakan DTL?

Kapan Menggunakan DTL?

Bagian 3: Algoritma Dasar (ID3)

Apa itu Algoritma ID3?

Alur Kerja ID3

Kapan ID3 Berhenti (Stopping Condition)?

Bagian 4: Matematika Inti (Entropy & Information Gain)

Bagaimana ID3 Memilih “Best Attribute”?

Apa itu Entropy?

Apa itu Information Gain?

Contoh Perhitungan (Play Tennis, hal 23-25)

Langkah Selanjutnya (Rekursif, hal 26)

Bagian 5: Latihan

Langkah 1: Hitung Entropy Awal (Parent S)

Langkah 2: Hitung Information Gain untuk Setiap Atribut

Langkah 3: Bandingkan Gain & Tentukan Root Node

Langkah 4: Proses Detail untuk Branch Ada Hangout? = Tidak

Bagian 5: Kelemahan DTL

Pendalaman 1: Masalah Terbesar ID3 - Overfitting

Pendalaman 2: Kelemahan Information Gain (Bias)

Pendalaman 3: Menangani Atribut Numerik (Kontinu)

Pendalaman 4: Dari ID3 ke Algoritma Modern

Graph View

Table of Contents

Backlinks

Langkah 1: Hitung Entropy Awal (Parent `S`)

Langkah 4: Proses Detail untuk Branch `Ada Hangout? = Tidak`