Density-based Clustering (DBSCAN)

Back to IF3170 Inteligensi Artifisial

Topic: 3. Density Based Clustering (DBSCAN)

Questions/Cues

• Filosofi Density-Based

• Parameter DBSCAN ($ϵ$, MinPts)

• Klasifikasi Titik (Core, Border, Noise)

• Konsep Reachability

• Studi Kasus (Perhitungan Manual)

• Algoritma DBSCAN (Flow)

• Kelebihan & Kekurangan

• Kompleksitas Algoritma

Reference Points

• Slide 36-39 (Konsep Dasar)

• Slide 40-42 (Klasifikasi Titik)

• Slide 43 (Algoritma)

• Slide 45-47 (Studi Kasus & Matriks)

1. Konsep Dasar Density-Based Clustering

Metode density-based mendekati masalah clustering dengan cara pandang yang berbeda total dari metode partisi (seperti K-Means).

Analogi Pulau:

Bayangkan data sebagai titik-titik lokasi orang di sebuah peta.

• Cluster adalah wilayah perkotaan yang padat penduduk.

• Noise adalah orang yang tinggal sendirian di hutan atau gurun (wilayah jarang).

• Jika Anda bisa berjalan dari satu rumah ke rumah lain tanpa pernah keluar dari “zona padat”, maka rumah-rumah itu berada di kota (cluster) yang sama.

Implikasi Penting:

1. Bentuk Fleksibel: Cluster bisa berbentuk apa saja (ular melingkar, huruf U, cincin), tidak harus bulat sferis.

2. Robust terhadap Outlier: Titik-titik di wilayah sepi otomatis dibuang sebagai noise, sehingga tidak merusak posisi pusat cluster (tidak seperti K-Means yang rata-ratanya bisa tertarik outlier).

2. Parameter Utama DBSCAN

Algoritma ini hanya membutuhkan dua parameter input untuk mendefinisikan apa itu “padat”:

1. Epsilon ($ϵ$): Jarak Pandang

   • Radius lingkaran maksimum di sekitar sebuah titik untuk mencari tetangga.

   • Semakin besar $ϵ$, semakin banyak titik yang dianggap bertetangga, cluster akan membesar dan menyatu.

2. MinPts (Minimum Points): Ambang Kepadatan

   • Jumlah minimum titik (termasuk titik itu sendiri) yang harus ada dalam radius $ϵ$ agar wilayah tersebut dianggap “Core” (padat).

   • Semakin besar MinPts, semakin ketat syarat kepadatan, semakin banyak data yang mungkin dianggap noise.

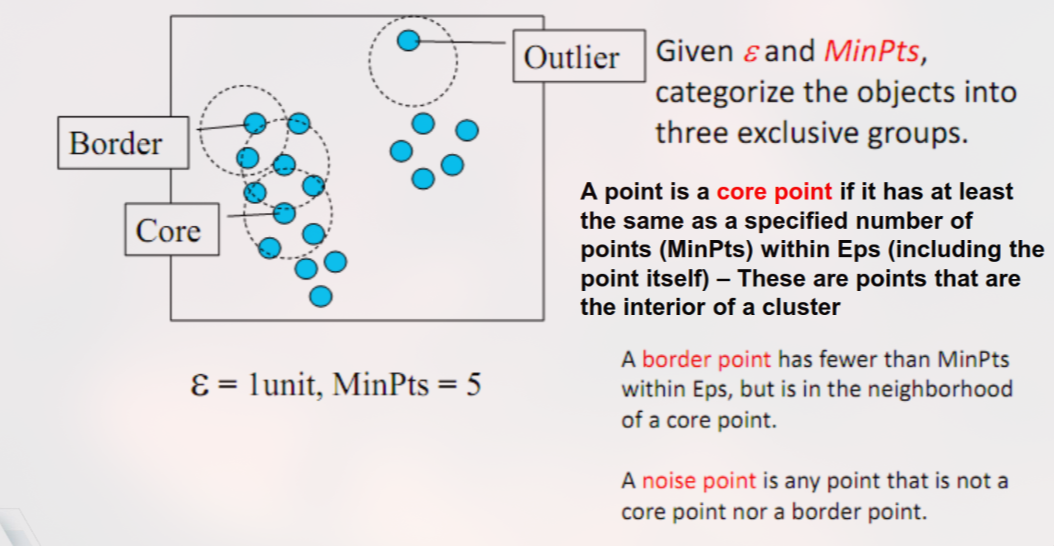
3. Klasifikasi Status Titik (Point Classification)

Berdasarkan dua parameter di atas, setiap titik dalam dataset akan diberi label:

Tipe Titik	Simbol Visual	Definisi Teknis	Peran
Core Point (Inti)	🟢 (Hijau)	Punya tetangga $\ge$ MinPts dalam radius $ϵ$.	Jantung cluster. Bisa “menularkan” keanggotaan cluster ke segala arah.
Border Point (Batas)	🔵 (Biru)	Punya tetangga $<$ MinPts, TAPI salah satu tetangganya adalah Core Point.	Pinggiran cluster. Menjadi anggota cluster tapi tidak bisa memperluas cluster lebih jauh.
Noise / Outlier	🔴 (Merah)	Bukan Core dan bukan Border. Tidak punya tetangga Core.	Data sampah. Dibuang/diabaikan.

Gambar 1	Gambar 2

4. Studi Kasus: Implementasi Langkah-demi-Langkah (Slide 45)

Skenario: Kita memiliki 8 titik data ($A1$ s.d $A8$). Matriks di bawah ini menunjukkan Jarak Kuadrat ($d^2$) antar titik.

Parameter:

• $ϵ=2\to$ Artinya jarak kuadrat maksimum ${ϵ}^2=4$.

• $MinPts=2$ (Sesuai slide 45, jika Epsilon=2, MinPoints=2).

Data Masukan (Matriks Jarak Kuadrat):

Nilai di sel adalah $distanc{e}^2$. Kita mencari nilai $\le 4$.

Titik	A1	A2	A3	A4	A5	A6	A7	A8
A1	0	25	72	13	50	52	65	5
A2	25	0	37	18	25	17	10	20
A3	72	37	0	25	2	4	53	41
A4	13	18	25	0	13	17	52	2
A5	50	25	2	13	0	2	45	25
A6	52	17	4	17	2	0	29	29
A7	65	10	53	52	45	29	0	58
A8	5	20	41	2	25	29	58	0

Langkah 1: Identifikasi Tetangga & Status Titik

Cek setiap baris. Hitung berapa banyak sel yang nilainya $\le 4$ (termasuk dirinya sendiri yang bernilai 0).

Titik	Tetangga (Jarak${}^2\le 4$)	Jumlah (N)	Status (N≥2?)	Keterangan
A1	{A1}	1	NOISE	Kurang dari MinPts.
A2	{A2}	1	NOISE	Kurang dari MinPts.
A3	{A3, A5, A6}	3	CORE	Jumlah $\ge 2$. Pusat kepadatan.
A4	{A4, A8}	2	CORE	Jumlah $\ge 2$.
A5	{A5, A3, A6}	3	CORE	Jumlah $\ge 2$.
A6	{A6, A3, A5}	3	CORE	Jumlah $\ge 2$.
A7	{A7}	1	NOISE	Kurang dari MinPts.
A8	{A8, A4}	2	CORE	Jumlah $\ge 2$.

Langkah 2: Pembentukan Cluster (Ekspansi)

Kita iterasi titik Core untuk membentuk “pulau”.

• Mulai dari A3 (Core):

  • Buat Cluster 1. Anggota awal: {A3}.

  • Cek tetangga A3: {A5, A6}. Masukkan ke antrian.

  • Proses A5: A5 adalah Core? Ya. Ambil tetangganya ({A3, A6}). Semua sudah di antrian. Masukkan A5 ke Cluster 1.

  • Proses A6: A6 adalah Core? Ya. Ambil tetangganya ({A3, A5}). Semua sudah di antrian. Masukkan A6 ke Cluster 1.

  • Antrian habis.

  • Hasil Cluster 1: {A3, A5, A6}.

• Lanjut ke Core berikutnya yang belum dikunjungi (misal A4):

  • Buat Cluster 2. Anggota awal: {A4}.
  • Cek tetangga A4: {A8}. Masukkan ke antrian.
  • Proses A8: A8 adalah Core? Ya. Ambil tetangganya ({A4}). Sudah di Cluster 2. Masukkan A8 ke Cluster 2.
  • Antrian habis.
  • Hasil Cluster 2: {A4, A8}.

• Sisa Titik (A1, A2, A7):

  • Status awal Noise. Cek apakah mereka tetangga dari Core?

  • A1 tetangga siapa? Cuma A1. Tetap Noise.

  • A2 tetangga siapa? Cuma A2. Tetap Noise.

  • A7 tetangga siapa? Cuma A7. Tetap Noise.

Kesimpulan Akhir Studi Kasus:

• Cluster 1: {A3, A5, A6}

• Cluster 2: {A4, A8}

• Outlier: {A1, A2, A7}

5. Konsep Reachability (Konektivitas)

Bagaimana DBSCAN tahu A terhubung ke B?

1. Directly Density-Reachable: A tetangga langsung B, dan B adalah Core Point. (Arah: B $\to$ A).

2. Density-Reachable: A terhubung ke B lewat rantai Core Points. (B $\to$ C $\to$ D $\to$ A).

3. Density-Connected: A dan B mungkin bukan Core, tapi keduanya bisa dijangkau dari satu Core Point O yang sama. (A $\leftarrow$ O $\to$ B). Ini mendefinisikan satu cluster utuh.

6. Analisis Kelebihan & Kekurangan

Kelebihan DBSCAN	Kekurangan DBSCAN
Bentuk Arbitrer: Bisa mendeteksi cluster bentuk cincin, spiral, ular, dll.	Sensitif Parameter: Sangat sulit menentukan $ϵ$ dan MinPts yang tepat tanpa pengetahuan domain.
Otomatis Deteksi Outlier: Noise dipisahkan, tidak merusak rata-rata cluster.	Variasi Densitas: Gagal jika data memiliki cluster dengan kepadatan yang jauh berbeda (misal satu sangat padat, satu agak renggang).
Tanpa Input K: Tidak perlu menebak jumlah cluster ($k$) di awal.	Curse of Dimensionality: Perhitungan jarak menjadi kurang bermakna pada dimensi sangat tinggi.

Summary

DBSCAN adalah algoritma clustering yang mendefinisikan cluster sebagai wilayah dengan kepadatan titik data yang tinggi. Menggunakan parameter Epsilon (jarak) dan MinPts (kepadatan), algoritma ini mengklasifikasikan titik menjadi Core (pusat), Border (pinggir), dan Noise (sampah). Dalam studi kasus manual, DBSCAN terbukti mampu mengelompokkan data yang saling berdekatan ({A3, A5, A6} dan {A4, A8}) secara alami dan mengisolasi titik-titik yang jauh ({A1, A2, A7}) sebagai noise, sesuatu yang sulit dilakukan K-Means tanpa merusak posisi centroid. Keunggulan utamanya adalah fleksibilitas bentuk cluster dan ketahanan terhadap outlier.

Ad Libitum: Pendalaman Teknis

1. Kompleksitas Waktu & Spatial Indexing

Secara naif, untuk setiap titik kita harus menghitung jarak ke semua titik lain.

• Time Complexity (Naive): $O(n^2)$. Ini lambat untuk data besar.

• Optimasi (Spatial Indexing): Jika menggunakan struktur data spasial seperti R-tree atau k-d tree untuk pencarian tetangga (range query).

• Time Complexity (Optimized): Turun menjadi $O(n\log n)$. Ini membuat DBSCAN cukup skalabel untuk dataset menengah-besar dengan dimensi rendah.

2. Menentukan Epsilon dengan k-Distance Graph

Cara heuristik standar untuk mencari $ϵ$:

1. Tetapkan $k=MinPts$.

2. Untuk setiap titik data, hitung jarak ke tetangga terdekat ke-k.

3. Urutkan jarak-jarak tersebut secara ascending.

4. Plot grafiknya. Akan terlihat kurva yang naik perlahan lalu melonjak tajam.

5. Titik lonjakan (“siku” atau knee) adalah nilai $ϵ$ yang optimal. Wilayah di bawah siku adalah cluster, wilayah di atas siku adalah noise.

3. Mengapa tidak bisa menangani Variasi Densitas?

Bayangkan dua cluster: Cluster A sangat padat (butuh $ϵ=1$), Cluster B agak renggang (butuh $ϵ=5$).

• Jika kita set $ϵ=1$: Cluster A terdeteksi, Cluster B dianggap noise semua.

• Jika kita set $ϵ=5$: Cluster B terdeteksi, tapi Cluster A mungkin tergabung dengan noise di sekitarnya atau bergabung dengan cluster lain karena jarak pandang terlalu jauh.

• Solusi: Gunakan algoritma OPTICS (Ordering Points To Identify the Clustering Structure) yang merupakan pengembangan DBSCAN untuk variasi densitas.

Spaced Repetition Questions (Review)

1. Jika saya memiliki data berbentuk cincin melingkar, algoritma mana yang harus saya pilih: K-Means atau DBSCAN? Mengapa?

DBSCAN. K-Means hanya bisa mendeteksi cluster berbentuk cembung (convex/bulat) karena menggunakan centroid rata-rata. DBSCAN bisa mengikuti kontur kepadatan data, sehingga sukses mendeteksi bentuk cincin.

2. Apa yang terjadi jika nilai Epsilon terlalu kecil?

Data akan dianggap “jarang” semua. Sebagian besar data akan diklasifikasikan sebagai Noise, dan cluster yang terbentuk akan pecah menjadi cluster-cluster kecil yang tidak bermakna.

3. Bisakah Border Point menjadi titik awal pembentukan cluster?

Tidak. Cluster hanya bisa dimulai dari Core Point. Border point hanya bisa “diangkut” masuk ke cluster jika ia bertetangga dengan Core Point yang sedang ekspansi.