Pengenalan dan Konsep Dasar SVM

Back to IF3170 Inteligensi Artifisial

Topic: Support Vector Machines (Part 1: Introduction & Fundamentals)

Questions/Cues

• Apa itu SVM?

• SVM vs Neural Network

• Konsep Linearly Separable

• Definisi Hyperplane

• Mengapa Perceptron lemah?

• Apa itu Margin?

• Definisi Support Vector

Reference Points

• Slides: 1-16

• Modul: Supervised Learning

1. Pengenalan & Sejarah SVM

Support Vector Machine (SVM) adalah algoritma supervised learning untuk klasifikasi (dan regresi) yang diperkenalkan pada tahun 1992 oleh Vapnik, Boser, & Guyon.

Konteks Sejarah & Perbandingan:

• Era 1980-an (Neural Networks): NN populer karena bisa menangani data non-linear. Namun, NN memiliki kelemahan teoretis: bersifat heuristic/greedy dan rentan terjebak di local minima (solusi yang “cukup baik” tapi bukan yang terbaik).

• Era 1990-an (SVM): SVM muncul dengan landasan Teori Pembelajaran Komputasi (Computational Learning Theory) yang kuat. Keunggulan utamanya adalah penggunaan optimasi kuadratik (Quadratic Programming), yang menjamin ditemukannya global optimum (solusi matematika terbaik yang mutlak).

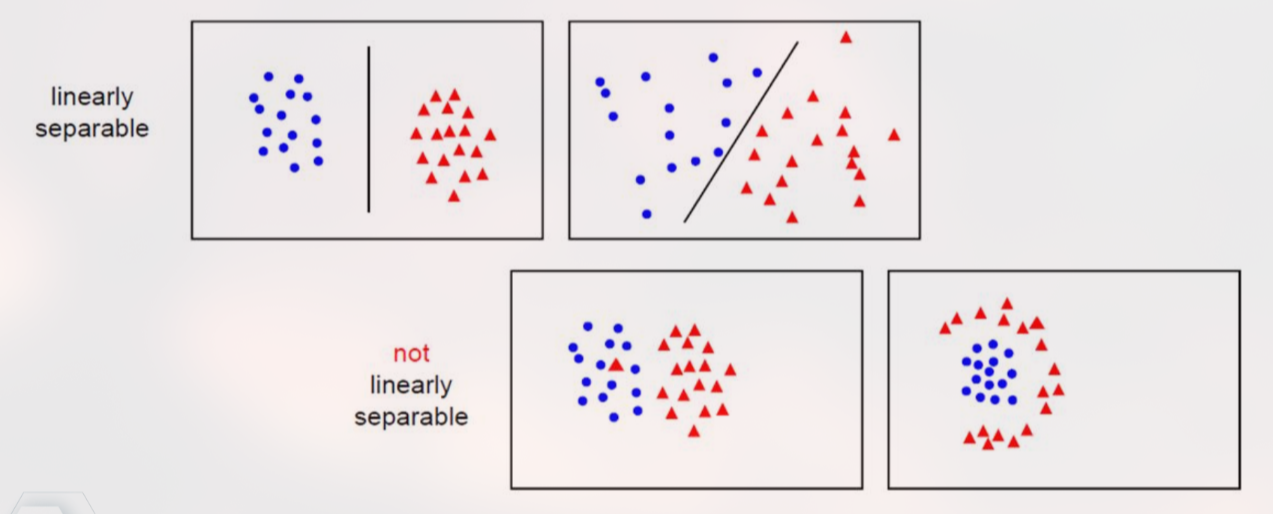
2. Klasifikasi Biner & Linear Separability

SVM fokus pada pemisahan data menjadi dua kelas ($+1$ dan $-1$).

• Linearly Separable: Kondisi di mana data dari dua kelas yang berbeda dapat dipisahkan secara sempurna oleh sebuah garis lurus (pada 2D) atau bidang datar (pada dimensi tinggi).

  

• Fungsi Keputusan: Kita mencari fungsi $f(x)$ di mana:

  • $f(x_i)\ge 0$ untuk kelas $+1$

  • $f(x_i)<0$ untuk kelas $-1$

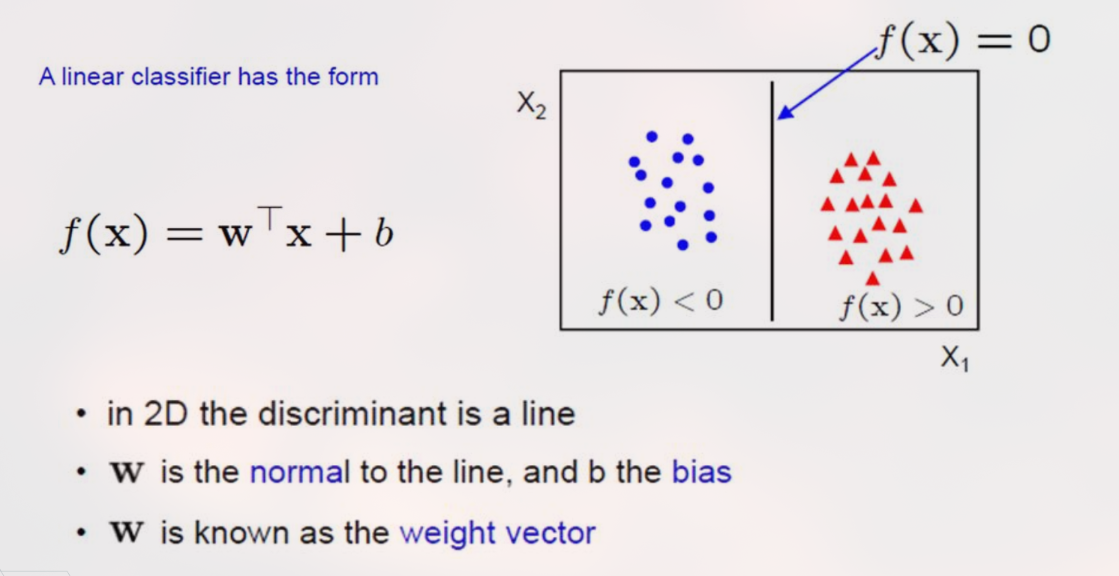
3. Konsep Hyperplane (Bidang Pemisah)

Batas keputusan dalam SVM disebut Hyperplane.

• Dimensi: Garis (di 2D), Bidang (di 3D), atau Hyperplane (di dimensi $n$).

• Persamaan Matematis:

  $f(x)=w^{T}x+b$

  • $w$ (Weight Vector): Vektor normal yang menentukan orientasi/arah permukaan hyperplane.

  • $b$ (Bias): Menentukan posisi hyperplane relatif terhadap titik asal (origin).

  • $x$: Vektor fitur data input.

Sifat Linear Classifier: Setelah proses training selesai dan nilai optimal $w$ dan $b$ ditemukan, data latih tidak lagi dibutuhkan untuk klasifikasi (berbeda dengan k-NN yang harus menyimpan semua data).

4. Perceptron vs SVM (Isu Generalisasi)

Mengapa kita butuh SVM jika Perceptron juga bisa membuat garis pemisah?

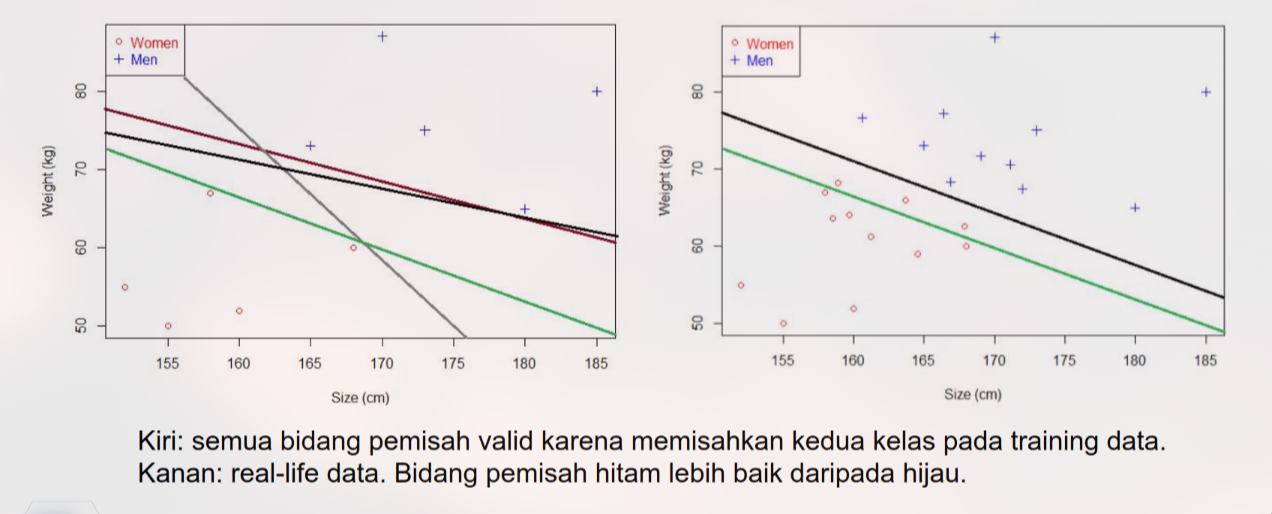
• Kelemahan Perceptron: Algoritma ini berhenti segera setelah menemukan sembarang garis yang memisahkan data tanpa error. Garis ini bisa saja sangat mepet dengan salah satu kelas.

• Masalah: Jika ada data baru yang sedikit berbeda (noise/variasi), garis yang mepet tadi kemungkinan besar akan salah memprediksi. Ini disebut generalisasi yang buruk.

5. Tujuan Utama SVM: Maximum Margin

SVM bertujuan mencari Optimal Separating Hyperplane, yaitu pemisah yang memiliki Margin Terbesar.

• Margin: Jarak tegak lurus antara hyperplane dengan titik data terdekat dari masing-masing kelas.

• Filosofi: “Zona aman” yang lebar (margin besar) memberikan toleransi kesalahan yang lebih baik saat menghadapi data baru yang belum pernah dilihat sebelumnya.

6. Support Vectors

Titik-titik data yang berada paling dekat dengan hyperplane (tepat di pinggir margin) disebut Support Vectors.

• Titik-titik inilah yang “menyangga” atau menentukan posisi hyperplane.

• Data lain yang jauh dari margin tidak berpengaruh pada model.

Summary

Support Vector Machine (SVM) adalah algoritma klasifikasi robust yang mengatasi kelemahan local minima pada Neural Network dan generalisasi buruk pada Perceptron. SVM bekerja dengan mencari Hyperplane Optimal ($w^{T}x+b=0$) yang memisahkan dua kelas data dengan Margin Terbesar. Kunci dari performa SVM terletak pada Support Vectors, yaitu subset data latih yang berada paling dekat dengan batas keputusan dan secara efektif menentukan posisi optimal hyperplane tersebut.

Ad Libitum: Pendalaman Teknis & Matematika

1. Matematika di Balik Proyeksi Vektor

Untuk memahami orientasi hyperplane, kita perlu meninjau konsep vektor dasar:

• Dot Product (Perkalian Titik):

  $u\cdot v=||u||||v||cos(\theta )$

• Direction Cosines: Arah sebuah vektor $u$ dapat didefinisikan oleh kosinus sudutnya terhadap sumbu koordinat:

  $cos(\theta )=\frac{u_1}{||u||},cos(\alpha )=\frac{u_2}{||u||}$

2. Geometri Hyperplane $w\cdot x+b=0$

Mengapa rumus ini merepresentasikan sebuah bidang datar?

• Vektor $w$ adalah vektor normal (tegak lurus) terhadap permukaan hyperplane.

• Ambil dua titik sembarang $x_1$ dan $x_2$ yang terletak pada hyperplane. Maka vektor $(x_1-x_2)$ terletak sejajar dengan hyperplane.

• Karena $w$ tegak lurus terhadap hyperplane, maka $w$ juga tegak lurus terhadap $(x_1-x_2)$.

• Secara matematis: $w\cdot (x_1-x_2)=0$. Inilah yang mendasari persamaan linear tersebut.

3. Intuisi “Support Vector”

Mengapa disebut “Support”? Bayangkan sebuah papan kayu (hyperplane) yang ditahan agar tidak jatuh. Papan itu hanya perlu ditopang oleh beberapa tiang penyangga (support vectors) yang posisinya paling krusial. Tiang-tiang lain yang jauh di belakang tidak memberikan kontribusi pada posisi papan tersebut. Ini membuat SVM efisien dalam memori karena model akhirnya hanya bergantung pada sebagian kecil data latih.

Spaced Repetition Questions (Review)

Cobalah untuk menjawab pertanyaan di bawah ini tanpa melihat catatan terlebih dahulu.

1. Apa perbedaan mendasar antara cara Perceptron dan SVM dalam memilih garis pemisah (hyperplane)?

Perceptron memilih sembarang hyperplane asalkan bisa memisahkan data tanpa error (bisa jadi sangat mepet dengan data), sedangkan SVM mencari hyperplane yang memisahkan data dengan margin terbesar (jarak terjauh dari data terdekat) untuk generalisasi yang lebih baik.

2. Apa yang dimaksud dengan "Support Vectors"?

Support Vectors adalah titik-titik data (dari masing-masing kelas) yang posisinya paling dekat dengan hyperplane. Mereka adalah titik-titik yang “menyangga” atau menentukan posisi dan orientasi hyperplane optimal.

3. Tuliskan persamaan matematis untuk Linear Classifier dalam SVM!

$f(x)=w^{T}x+b$

Dimana $w$ adalah vektor bobot (arah normal) dan $b$ adalah bias.

4. Mengapa SVM dikatakan memiliki dasar teoretis yang lebih kuat dibanding Neural Network klasik?

Karena SVM berbasis pada Computational Learning Theory dan menggunakan optimasi kuadratik (Convex Optimization) yang menjamin ditemukannya Global Optimum, berbeda dengan NN yang rentan terjebak di Local Minima.

5. Apa yang terjadi pada data latih setelah model SVM Linear selesai dilatih (mendapatkan nilai w dan b)?

Data latih dapat dibuang (discarded), karena klasifikasi data baru hanya membutuhkan nilai vektor $w$ dan bias $b$, tidak perlu membandingkan dengan seluruh data latih seperti pada k-NN.

6. Jelaskan kondisi "Linearly Separable"!

Kondisi di mana data dari dua kelas yang berbeda dapat dipisahkan secara sempurna (tanpa error) oleh sebuah garis lurus (2D) atau bidang datar (dimensi tinggi).