SVM Untuk Linearly Separable Data

Back to IF3170 Inteligensi Artifisial

Topic: SVM for Linearly Separable Data (Mathematics & Optimization)

Questions/Cues

• Definisi Matematis Support Vector

• Persamaan Bidang Pembatas

• Rumus Lebar Margin

• Fungsi Objektif SVM

• Quadratic Programming (QP)

• Primal vs Dual Problem

• Peran Lagrange Multiplier (Alpha)

• Cara menghitung bias (b)

Reference Points

• Slides: 17-38

• Modul: Supervised Learning

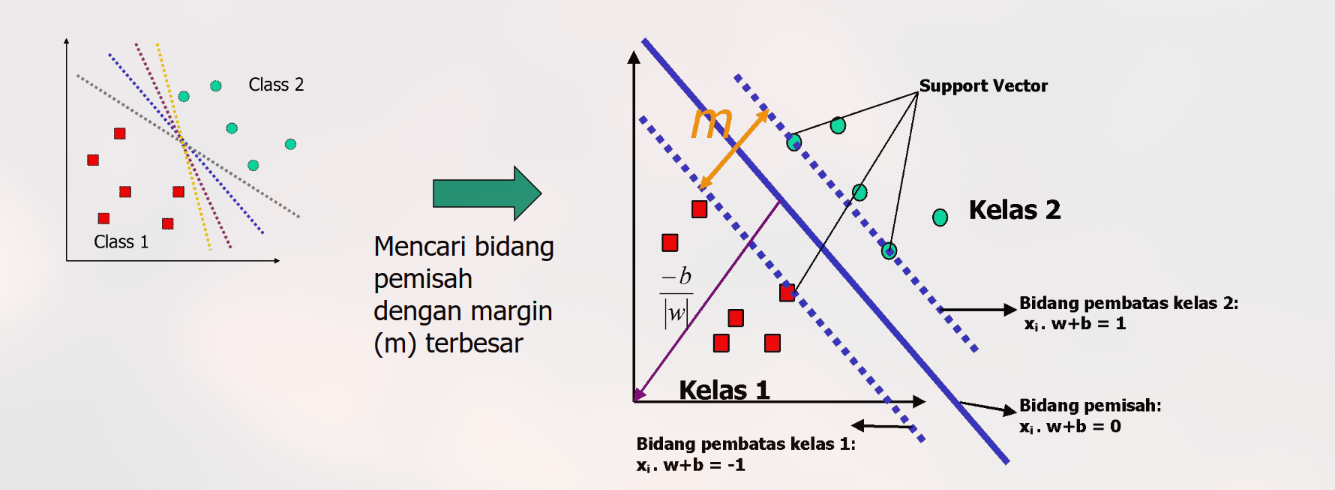
1. Definisi Formal Support Vector & Margin

Pada data yang linearly separable (dapat dipisahkan sempurna secara linear), SVM mencari dua bidang pembatas paralel yang memisahkan data dengan jarak terjauh.

Persamaan Bidang:

• Hyperplane Tengah (Pemisah): $w\cdot x+b=0$

• Pembatas Kelas +1: $w\cdot x+b=+1$ (Data di garis ini labelnya +1)

• Pembatas Kelas -1: $w\cdot x+b=-1$ (Data di garis ini labelnya -1)

Kondisi Matematis:

Agar klasifikasi benar dan berada di luar margin, seluruh data latih harus memenuhi pertidaksamaan:

$y_i(w\cdot x_i+b)\ge 1$

• Jika hasilnya $=1$, maka data tersebut berada tepat di garis pembatas. Data inilah yang disebut Support Vector.

• Jika hasilnya $>1$, maka data berada di zona aman (bukan support vector).

2. Optimasi Margin (Objective Function)

Tujuan SVM adalah memaksimalkan lebar margin ($m$).

Rumus Lebar Margin:

Jarak tegak lurus antara pembatas kelas +1 dan -1 adalah:

$Margin=\frac{2}{||w||}$

Masalah Optimasi: Untuk memaksimalkan margin, kita harus meminimalkan $||w||$.

Secara matematis, untuk memudahkan penurunan rumus (agar bisa diturunkan/derivative), kita meminimalkan kuadratnya:

Primal Problem (Masalah Asli):

$Minimize:\frac{1}{2}||w|{|}^2$

Subject to: $y_i(w\cdot x_i+b)\ge 1$ (Semua data harus benar di luar margin).

Ini adalah masalah Convex Quadratic Programming (QP).

3. Lagrange Multipliers & Dual Problem

Masalah optimasi di atas (Primal) sulit diselesaikan langsung karena ada kendala pertidaksamaan. Kita mengubahnya menjadi masalah Dual menggunakan metode Lagrange Multipliers.

Transformasi ke Dual Problem:

Kita memperkenalkan variabel baru bernama Alpha (${\alpha }_i$) untuk setiap titik data.

Fungsi Dual yang Harus Dimaksimalkan:

$Maximize:{\sum }_{i=1}^n{\alpha }_i-\frac{1}{2}{\sum }_{i=1}^n{\sum }_{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)$

Kendala Baru:

1. $\sum {\alpha }_i{y}_i=0$

2. ${\alpha }_i\ge 0$

Keuntungan Bentuk Dual:

Masalah kini hanya bergantung pada Dot Product $(x_i\cdot x_j)$ antar data latih. Ini sangat krusial untuk menangani data non-linear nanti (menggunakan Kernel Trick).

4. Interpretasi Nilai Alpha ($\alpha$)

Setelah masalah optimasi diselesaikan (biasanya menggunakan software QP Solver), kita mendapatkan nilai $\alpha$ untuk setiap data.

• Jika ${\alpha }_i=0$: Data tersebut bukan Support Vector. Data ini tidak berpengaruh pada pembentukan garis pemisah.

• Jika ${\alpha }_i>0$: Data tersebut adalah Support Vector. Data ini terletak tepat di batas margin ($y_i(w\cdot x+b)=1$).

5. Menghitung Model Akhir ($w$ dan $b$)

Setelah nilai $\alpha$ ditemukan:

1. Hitung Bobot ($w$):

   $w={\sum }_{i=1}^n{\alpha }_i{y}_i{x}_i$

   (Hanya support vector yang berkontribusi karena $\alpha$ lainnya 0).

2. Hitung Bias ($b$):

   Ambil salah satu support vector ($x_{sv},y_{sv}$), lalu masukkan ke persamaan:

   $b=y_{sv}-w\cdot x_{sv}$

   (Dalam prakteknya, sering dirata-rata dari semua support vector untuk kestabilan numerik).

3. Fungsi Klasifikasi Baru:

   $f(x)=sign({\sum }_{i=1}^n{\alpha }_i{y}_i(x_i\cdot x)+b)$

6. Studi Kasus Perhitungan Manual (Step-by-Step)

Dataset 2D Sederhana:

Kita punya 3 data latih.

• Kelas Positif (+1): $x_1=(3,3)$, $x_2=(4,3)$

• Kelas Negatif (-1): $x_3=(1,1)$

Analisis Visual: $x_1$ paling dekat dengan $x_3$, kemungkinan besar mereka adalah Support Vector. $x_2$ ada di belakang $x_1$.

Langkah 1: Hitung Dot Product ($x_i\cdot x_j$)

Rumus: $A\cdot B=(A_1{B}_1+A_2{B}_2)$

Perkalian	Pasangan Data	Perhitungan	Hasil
$x_1\cdot x_1$	$(3,3)\cdot (3,3)$	$9+9$	18
$x_1\cdot x_2$	$(3,3)\cdot (4,3)$	$12+9$	21
$x_1\cdot x_3$	$(3,3)\cdot (1,1)$	$3+3$	6
$x_2\cdot x_2$	$(4,3)\cdot (4,3)$	$16+9$	25
$x_2\cdot x_3$	$(4,3)\cdot (1,1)$	$4+3$	7
$x_3\cdot x_3$	$(1,1)\cdot (1,1)$	$1+1$	2

Langkah 2: Menyusun Persamaan Dual

Kendala: ${\alpha }_1(1)+{\alpha }_2(1)+{\alpha }_3(-1)=0\Rightarrow {\alpha }_1+{\alpha }_2={\alpha }_3$.

Asumsi: $x_2$ jauh di belakang, jadi bukan support vector. Set ${\alpha }_2=0$.

Maka: ${\alpha }_1={\alpha }_3=\alpha$.

Masukkan ke Fungsi $L(\alpha )$:

L = (\alpha_1 + \alpha_3) - \frac{1}{2} [ \alpha_1^2 y_1 y_1 (x_1 \cdot x_1) + \alpha_3^2 y_3 y_3 (x_3 \cdot x_3) + 2 \alpha_1 \alpha_3 y_1 y_3 (x_1 \cdot x_3) ]$$$$L = 2\alpha - \frac{1}{2} [ \alpha^2(1)(18) + \alpha^2(1)(2) + 2(\alpha)(\alpha)(-1)(6) ]$$$$L = 2\alpha - \frac{1}{2} [ 18\alpha^2 + 2\alpha^2 - 12\alpha^2 ]$$$$L = 2\alpha - \frac{1}{2} [ 8\alpha^2 ] = 2\alpha - 4\alpha^2

Langkah 3: Cari Alpha Optimal

Turunkan terhadap $\alpha$ dan samakan dengan 0:

$\frac{dL}{d\alpha }=2-8\alpha =0\Rightarrow 8\alpha =2\Rightarrow \alpha =0.25$

• ${\alpha }_1=0.25$ (Support Vector)

• ${\alpha }_3=0.25$ (Support Vector)

• ${\alpha }_2=0$ (Bukan)

Langkah 4: Hitung Bobot ($w$)

$w=\sum {\alpha }_i{y}_i{x}_i$

$w={\alpha }_1{y}_1{x}_1+{\alpha }_3{y}_3{x}_3$

$w=0.25(1)(3,3)+0.25(-1)(1,1)$

$w=(0.75,0.75)-(0.25,0.25)=(0.5,0.5)$

Langkah 5: Hitung Bias ($b$)

Gunakan salah satu Support Vector (misal $x_1$).

$w\cdot x_1+b=y_1$

$(0.5,0.5)\cdot (3,3)+b=1$

$(1.5+1.5)+b=1$

$3+b=1\Rightarrow \mathbf{b}=-2$

Langkah 6: Persamaan Akhir & Verifikasi

Fungsi Keputusan: $f(x)=0.5x_1+0.5x_2-2$

Uji Data	Perhitungan	Hasil	Target	Status
$x_1(3,3)$	$0.5(3)+0.5(3)-2$	1	+1	Support Vector
$x_2(4,3)$	$0.5(4)+0.5(3)-2$	1.5	+1	Benar (>1)
$x_3(1,1)$	$0.5(1)+0.5(1)-2$	-1	-1	Support Vector

7. Studi Kasus 2 (PPT)

Dataset

x1	x2	Kelas
3	1	+1
3	-1	+1
6	1	+1
6	-1	+1
1	0	-1
0	1	-1
0	-1	-1
-1	0	-1

---

Identifikasi Support Vectors

Dari visualisasi data, titik-titik yang paling dekat antar kelas (yang berada di perbatasan) adalah:

Support Vectors yang dipilih:

• SV1: (1, 0) dengan kelas -1
• SV2: (3, 1) dengan kelas +1
• SV3: (3, -1) dengan kelas +1

Titik-titik ini ditandai dengan lingkaran kuning pada plot.

---

Langkah 1: Menyusun Persamaan dari Syarat Support Vector

Untuk Support Vector, berlaku:

$f(\vec{x})={\sum }_{i=1}^{nsv}({\alpha }_i{y}_i{\vec{x}}_i\cdot \vec{x})+b=y$

Kita akan menyusun persamaan untuk ketiga support vector:

Persamaan 1: Titik (1, 0) → Kelas -1

$f\left(\begin{array}{c}1\\ 0\end{array}\right)\Rightarrow -1={\alpha }_1\cdot (-1)\left(\begin{array}{c}1\\ 0\end{array}\right)\cdot \left(\begin{array}{c}1\\ 0\end{array}\right)+{\alpha }_2\cdot 1\left(\begin{array}{c}3\\ 1\end{array}\right)\cdot \left(\begin{array}{c}1\\ 0\end{array}\right)+{\alpha }_3\cdot 1\left(\begin{array}{c}3\\ -1\end{array}\right)\cdot \left(\begin{array}{c}1\\ 0\end{array}\right)+b$

$=-{\alpha }_1+3{\alpha }_2+3{\alpha }_3+b\dots (1)$

Persamaan 2: Titik (3, 1) → Kelas +1

$f\left(\begin{array}{c}3\\ 1\end{array}\right)\Rightarrow 1={\alpha }_1\cdot (-1)\left(\begin{array}{c}1\\ 0\end{array}\right)\cdot \left(\begin{array}{c}3\\ 1\end{array}\right)+{\alpha }_2\cdot 1\left(\begin{array}{c}3\\ 1\end{array}\right)\cdot \left(\begin{array}{c}3\\ 1\end{array}\right)+{\alpha }_3\cdot 1\left(\begin{array}{c}3\\ -1\end{array}\right)\cdot \left(\begin{array}{c}3\\ 1\end{array}\right)+b$

$=-3{\alpha }_1+10{\alpha }_2+8{\alpha }_3+b\dots (2)$

Persamaan 3: Titik (3, -1) → Kelas +1

$f\left(\begin{array}{c}3\\ -1\end{array}\right)\Rightarrow 1={\alpha }_1\cdot (-1)\left(\begin{array}{c}1\\ 0\end{array}\right)\cdot \left(\begin{array}{c}3\\ -1\end{array}\right)+{\alpha }_2\cdot 1\left(\begin{array}{c}3\\ 1\end{array}\right)\cdot \left(\begin{array}{c}3\\ -1\end{array}\right)+{\alpha }_3\cdot 1\left(\begin{array}{c}3\\ -1\end{array}\right)\cdot \left(\begin{array}{c}3\\ -1\end{array}\right)+b$

$=-3{\alpha }_1+8{\alpha }_2+10{\alpha }_3+b\dots (3)$

Persamaan 4: Constraint SVM

$\sum {\alpha }_i{y}_i=0$

$-{\alpha }_1+{\alpha }_2+{\alpha }_3=0\dots (4)$

---

Langkah 2: Penyelesaian Sistem Persamaan Linear

Sistem persamaan yang harus diselesaikan:

$-{\alpha }_1+3{\alpha }_2+3{\alpha }_3+b=-1\dots (1)$ $-3{\alpha }_1+10{\alpha }_2+8{\alpha }_3+b=1\dots (2)$ $-3{\alpha }_1+8{\alpha }_2+10{\alpha }_3+b=1\dots (3)$ $-{\alpha }_1+{\alpha }_2+{\alpha }_3=0\dots (4)$

Eliminasi (2) dan (3):

$(2)-(3):2{\alpha }_2-2{\alpha }_3=0\to {\alpha }_2={\alpha }_3\dots (5)$

Substitusi (5) ke (1) dan (2):

Dari (1): $-{\alpha }_1+3{\alpha }_2+3{\alpha }_2+b=-1$ $-{\alpha }_1+6{\alpha }_2+b=-1\dots (6)$

Dari (2): $-3{\alpha }_1+10{\alpha }_2+8{\alpha }_2+b=1$ $-3{\alpha }_1+18{\alpha }_2+b=1\dots (7)$

Eliminasi (6) dan (7):

$(6)-(7):2{\alpha }_1-12{\alpha }_2=-2$ ${\alpha }_1-6{\alpha }_2=-1$ ${\alpha }_1=6{\alpha }_2-1\dots (8)$

Substitusi (5) dan (8) ke constraint (4):

$-(6{\alpha }_2-1)+{\alpha }_2+{\alpha }_2=0$ $-6{\alpha }_2+1+2{\alpha }_2=0$ $-4{\alpha }_2=-1$ ${\alpha }_2=\frac{1}{4}=0.25$

Cari variabel lainnya:

${\alpha }_3={\alpha }_2=0.25$ ${\alpha }_1=6(0.25)-1=1.5-1=0.5$

Substitusi ke (6) untuk mencari b:

$-0.5+6(0.25)+b=-1$ $-0.5+1.5+b=-1$ $1+b=-1$ $b=-2$

---

Hasil Akhir

${\alpha }_1=0.5;{\alpha }_2=0.25;{\alpha }_3=0.25$ $b=-2$

Fungsi Hipotesis:

$f(\vec{x})={\sum }_{i=1}^{nsv}({\alpha }_i{y}_i{\vec{x}}_i\cdot \vec{x})-2$

dengan:

• α₁ = 0.5
• α₂ = α₃ = 0.25

---

Langkah 3: Pengujian Hipotesis

Uji dengan data baru: x = (6, 1)

$f\left(\begin{array}{c}6\\ 1\end{array}\right)=sign\left((0.5)(-1)\left(\begin{array}{c}1\\ 0\end{array}\right)\cdot \left(\begin{array}{c}6\\ 1\end{array}\right)+(0.25)(1)\left(\begin{array}{c}3\\ 1\end{array}\right)\cdot \left(\begin{array}{c}6\\ 1\end{array}\right)+(0.25)(1)\left(\begin{array}{c}3\\ -1\end{array}\right)\cdot \left(\begin{array}{c}6\\ 1\end{array}\right)-2\right)$

Hitung dot products:

• $(1,0)\cdot (6,1)=6$
• $(3,1)\cdot (6,1)=18+1=19$
• $(3,-1)\cdot (6,1)=18-1=17$

Substitusi:

$f\left(\begin{array}{c}6\\ 1\end{array}\right)=sign(-3+4.75+4.25-2)=sign(4)=1$

Hasil: Data (6, 1) diprediksi masuk kelas +1 ✓

---

Visualisasi Hasil

Hyperplane yang terbentuk memisahkan:

• Kelas -1 (kotak merah) di sebelah kiri
• Kelas +1 (titik biru) di sebelah kanan

Support Vectors (lingkaran kuning):

• (1, 0) dengan α₁ = 0.5
• (3, 1) dengan α₂ = 0.25
• (3, -1) dengan α₃ = 0.25

Garis hitam vertikal adalah hyperplane pemisah dengan persamaan yang didapat dari model SVM.

8. Studi Kasus 3: Perhitungan Kompleks (3 Support Vectors)

Dataset:

Data	x1​	x2​	Kelas (y)
$P_1$	3	1	+1
$P_2$	3	-1	+1
$P_3$	6	1	+1
$P_4$	6	-1	+1
$N_1$	1	0	-1
$N_2$	0	1	-1
$N_3$	0	-1	-1
$N_4$	-1	0	-1

Identifikasi Support Vectors:

Secara visual, data yang paling berdekatan antar kelas adalah:

• Kelas -1: Titik terluar kanan $\to$ $N_1(1,0)$. (Kita sebut ini data ke-1 untuk perhitungan, $y_1=-1$)

• Kelas +1: Titik terluar kiri $\to$ $P_1(3,1)$ dan $P_2(3,-1)$. (Kita sebut ini data ke-2 dan ke-3, $y_2=1,y_3=1$).

Langkah 1: Menyusun Persamaan dari Syarat SV

Untuk Support Vector, berlaku $f(\vec{x})=y_i$.

Rumus: $\sum ({\alpha }_j{y}_j{\vec{x}}_j\cdot {\vec{x}}_i)+b=y_i$.

Kita akan menyusun persamaan berdasarkan 3 titik yang diduga SV:

1. Titik 1 $(1,0)$ (Kelas -1):

   ${\alpha }_1(-1)(x_1\cdot x_1)+{\alpha }_2(1)(x_2\cdot x_1)+{\alpha }_3(1)(x_3\cdot x_1)+b=-1$

   $-{\alpha }_1(1)+{\alpha }_2(3)+{\alpha }_3(3)+b=-1\dots (1)$

2. Titik 2 $(3,1)$ (Kelas +1):

   ${\alpha }_1(-1)(x_1\cdot x_2)+{\alpha }_2(1)(x_2\cdot x_2)+{\alpha }_3(1)(x_3\cdot x_2)+b=1$

   $-{\alpha }_1(3)+{\alpha }_2(10)+{\alpha }_3(8)+b=1\dots (2)$

   (Note: $x_2\cdot x_2=3^2+1^2=10$, $x_3\cdot x_2=(3)(3)+(-1)(1)=8$)

3. Titik 3 $(3,-1)$ (Kelas +1):

   ${\alpha }_1(-1)(x_1\cdot x_3)+{\alpha }_2(1)(x_2\cdot x_3)+{\alpha }_3(1)(x_3\cdot x_3)+b=1$

   $-{\alpha }_1(3)+{\alpha }_2(8)+{\alpha }_3(10)+b=1\dots (3)$

4. Constraint SVM ($\sum {\alpha }_i{y}_i=0$):

   $-{\alpha }_1+{\alpha }_2+{\alpha }_3=0\dots (4)$

Langkah 2: Penyelesaian Sistem Persamaan Linear

• Eliminasi (2) dan (3):

  $(2)-(3)\Rightarrow 2{\alpha }_2-2{\alpha }_3=0\Rightarrow {\alpha }_2={\alpha }_3\dots (5)$

• Substitusi (5) ke (1) dan (2):

  (1) menjadi: $-{\alpha }_1+6{\alpha }_2+b=-1\dots (6)$

  (2) menjadi: $-3{\alpha }_1+18{\alpha }_2+b=1\dots (7)$

• Eliminasi (6) dan (7):

  (6) - (7) $\Rightarrow 2{\alpha }_1-12{\alpha }_2=-2\Rightarrow {\alpha }_1-6{\alpha }_2=-1$

  ${\alpha }_1=6{\alpha }_2-1\dots (8)$

• Substitusi (5) dan (8) ke Constraint (4):

  $-(6{\alpha }_2-1)+{\alpha }_2+{\alpha }_2=0$

  $-6{\alpha }_2+1+2{\alpha }_2=0$

  $-4{\alpha }_2=-1\Rightarrow {\alpha }_2=0.25$

• Cari variabel lain:

  ${\alpha }_3={\alpha }_2=0.25$

  ${\alpha }_1=6(0.25)-1=1.5-1=0.5$

  Substitusi ke (6): $-0.5+6(0.25)+b=-1\Rightarrow -0.5+1.5+b=-1\Rightarrow 1+b=-1\Rightarrow \mathbf{b}=-2$

Hasil Akhir Model:

${\alpha }_1=0.5,{\alpha }_2=0.25,{\alpha }_3=0.25,b=-2$.

Karena semua $\alpha >0$, ketiga titik tersebut benar merupakan Support Vectors.

Langkah 3: Pengujian Hipotesis

Misal ada data baru $x_{new}=(6,1)$. Prediksi kelasnya?

$f(x)=\sum ({\alpha }_i{y}_i{x}_i\cdot x_{new})+b$

$f(x)=[{\alpha }_1(-1)(x_1\cdot x_{new})]+[{\alpha }_2(1)(x_2\cdot x_{new})]+[{\alpha }_3(1)(x_3\cdot x_{new})]-2$

• $x_1\cdot x_{new}=(1,0)\cdot (6,1)=6$

• $x_2\cdot x_{new}=(3,1)\cdot (6,1)=18+1=19$

• $x_3\cdot x_{new}=(3,-1)\cdot (6,1)=18-1=17$

$f(x)=[0.5(-1)(6)]+[0.25(1)(19)]+[0.25(1)(17)]-2$

$f(x)=-3+4.75+4.25-2$

$f(x)=4$

Sign(4) = +1. (Data masuk kelas Positif).

Summary

Pada data Linearly Separable, SVM diformulasikan sebagai masalah Quadratic Programming (QP) dengan tujuan meminimalkan $||w|{|}^2$ (yang ekuivalen dengan memaksimalkan margin $2/||w||$) dengan kendala klasifikasi yang benar. Masalah ini diselesaikan menggunakan metode Lagrange Multipliers dalam bentuk Dual Problem, di mana kita mencari nilai ${\alpha }_i$. Hanya data dengan ${\alpha }_i>0$ yang menjadi Support Vectors dan menentukan bentuk hyperplane akhir.

Ad Libitum: Derivasi & Kalkulasi Detail

1. Mengapa Lebar Margin = $2/||w||$?

Misalkan kita punya dua hyperplane paralel:

$H_1:w\cdot x+b=1$

$H_2:w\cdot x+b=-1$

Ambil sembarang titik $x_1$ di $H_1$ dan $x_2$ di $H_2$. Jarak antara kedua bidang adalah proyeksi vektor $(x_1-x_2)$ pada vektor normal satuan $\frac{w}{||w||}$.

w \cdot x_1 = 1 - b$$$$w \cdot x_2 = -1 - b

Kurangi persamaan:

$w\cdot (x_1-x_2)=2$

Bagi kedua sisi dengan $||w||$:

$\frac{w}{||w||}\cdot (x_1-x_2)=\frac{2}{||w||}$

Sisi kiri adalah definisi jarak proyeksi. Maka terbukti lebar margin adalah $\frac{2}{||w||}$.

2. Contoh Perhitungan Manual (Sederhana)

Misal ada 3 titik 1D (Sesuai slide 33-36 tapi disederhanakan):

Kelas +1: $x=1$

Kelas -1: $x=3$

Support vector pasti di $x=1$ dan $x=3$.

Jaraknya 2 unit. Margin optimal harus di tengah ($x=2$).

Setengah lebar margin = 1.

Maka $Margin=2/w\to 2=2/w\to w=1$.

Cek Bias:

$w\cdot x+b=1$ (untuk kelas +1, $x=1$)

$1(1)+b=1\to b=0$.

Fungsi keputusan: $f(x)=x$.

Cek $x=1\to 1$ (Kelas +1). Cek $x=3\to 3$ (Kelas +1? Salah, harusnya -1).

Jika kelas kiri +1 dan kanan -1, maka $w$ harus negatif.

Perhitungan SVM yang benar akan otomatis menangani tanda +/- ini melalui optimasi $\alpha$.

Spaced Repetition Questions (Review)

Cobalah menjawab pertanyaan berikut untuk menguji pemahaman teknis Anda.

1. Apa hubungan antara meminimalkan ||w|| dengan margin?

Lebar margin didefinisikan sebagai $2/||w||$. Oleh karena itu, untuk memaksimalkan margin (membuat jalan pemisah selebar mungkin), kita harus meminimalkan penyebutnya, yaitu norma vektor bobot $||w||$.

2. Dalam solusi Dual Problem, apa arti jika sebuah data memiliki alpha = 0?

Jika ${\alpha }_i=0$, berarti data tersebut bukan Support Vector. Data ini berada jauh dari batas margin (di zona aman) dan tidak memiliki pengaruh apapun terhadap pembentukan garis keputusan (hyperplane).

3. Mengapa kita lebih memilih menyelesaikan SVM dalam bentuk Dual Problem daripada Primal Problem?

Karena dalam bentuk Dual, fungsi objektifnya hanya bergantung pada Dot Product antar data $(x_i\cdot x_j)$. Hal ini memungkinkan penggunaan Kernel Trick nantinya untuk menangani data yang tidak terpisah secara linear (non-linear).

4. Bagaimana persamaan kendala (constraint) SVM dituliskan secara matematis?

$y_i(w\cdot x_i+b)\ge 1$

Artinya, untuk semua data latih, hasil proyeksi dan bias harus setidaknya bernilai 1 (untuk kelas positif) atau setidaknya -1 (untuk kelas negatif, dikali $y_i$ jadi positif), yang menjamin data berada di luar margin.

5. Berapa banyak data yang biasanya memiliki alpha > 0 pada dataset yang besar?

Biasanya hanya sebagian kecil dari total data (sparse). Hanya titik-titik yang paling sulit diklasifikasikan (di perbatasan) yang memiliki \alpha > 0. Inilah yang membuat SVM efisien dalam memori untuk menyimpan model akhirnya.