SVM Untuk Non-Linearly Separable Data

Back to IF3170 Inteligensi Artifisial

Topic: SVM for Non-Linearly Separable Data (Soft Margin & Kernels)

Questions/Cues

• Penyebab Data Non-Linear

• Definisi Slack Variable

• Konsep Soft Margin

• Peran Parameter C

• Transformasi Dimensi

• Definisi Kernel Trick

• Jenis-jenis Kernel

• RBF Kernel

Reference Points

• Slides: 39-51

• Modul: Supervised Learning

1. Masalah Non-Linearly Separable

Dalam dunia nyata, data jarang sekali terpisah sempurna secara linear. Hal ini disebabkan oleh dua faktor utama:

• Noise: Data outlier atau kesalahan pengukuran yang membuat pemisahan sempurna tidak mungkin dilakukan tanpa overfitting.

• Sifat Alami Data: Pola data memang kompleks (misalnya melingkar) sehingga batasnya bukan garis lurus.

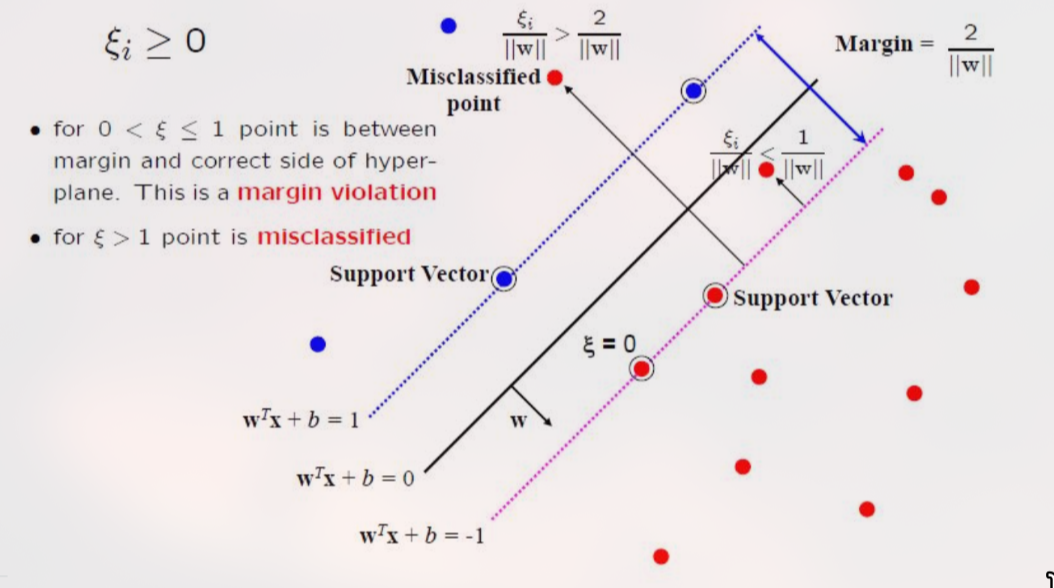
2. Solusi 1: Slack Variables (Soft Margin SVM)

Untuk menangani noise, SVM memodifikasi kendala (constraint) agar lebih longgar. Kita mengizinkan beberapa data salah diklasifikasikan atau masuk ke dalam margin.

• Slack Variable (${\xi }_i$): Variabel non-negatif yang mengukur seberapa jauh sebuah titik melanggar margin.

  • ${\xi }_i=0$: Data terklasifikasi benar dan di luar margin (aman).
  • $0<{\xi }_i\le 1$: Data berada di dalam margin tetapi masih di sisi yang benar.
  • ${\xi }_i>1$: Data salah diklasifikasikan (misclassified).

  

• Fungsi Objektif Baru: Kita tidak hanya meminimalkan $||w|{|}^2$, tapi juga meminimalkan total kesalahan ($\sum \xi$).

  $Minimize:\frac{1}{2}||w|{|}^2+C{\sum }_{i=1}^N{\xi }_i$

• Formulasi Dual Baru:

$Q(\alpha )=\sum {\alpha }_i-\frac{1}{2}\sum \sum {\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j$

Subject to: $0\le {\alpha }_i\le C$

Perhatikan: Rumus Dual-nya SAMA PERSIS dengan Hard Margin. Bedanya hanya pada batas atas ${\alpha }_i$ yang sekarang dibatasi oleh $C$.

3. Peran Parameter C (Regularization)

Parameter C adalah konstanta yang ditentukan pengguna untuk mengontrol trade-off antara margin yang lebar vs. kesalahan klasifikasi.

• C Besar (Strict):

  • Memberi hukuman berat pada setiap $\xi$. Model berusaha keras agar error = 0.

  • Akibat: Margin sempit, garis batas berlekuk-lekuk mengikuti data (potensi Overfitting).

• C Kecil (Tolerant):

  • Lebih santai terhadap error. Mengutamakan margin yang lebar meskipun ada beberapa data yang salah.

  • Akibat: Margin lebar, batas lebih sederhana (potensi Underfitting jika terlalu kecil, tapi lebih robust).

4. Solusi 2: Non-Linear Boundary Transformation

Jika data memiliki pola non-linear (misal: lingkaran), garis lurus tidak akan pernah bisa memisahkannya.

• Ide Utama: Petakan data dari dimensi rendah (Input Space) ke dimensi yang lebih tinggi (Feature Space) menggunakan fungsi pemetaan $\varphi (x)$.

• Contoh: Data 2D melingkar ($x_1,x_2$) dipetakan ke 3D ($z_1,z_2,z_3$) di mana $z_3=x_1^2+x_2^2$. Di dimensi 3D, data tersebut mungkin menjadi terpisah secara linear oleh sebuah bidang datar. Saat dikembalikan ke 2D, bidang datar itu menjadi garis lengkung (lingkaran).

5. The Kernel Trick

Menghitung transformasi $\varphi (x)$ ke dimensi sangat tinggi (bahkan tak hingga) itu mahal dan lambat.

Triknya:

Dalam optimasi Dual Problem, kita hanya butuh hasil Dot Product $(x_i\cdot x_j)$. Kita tidak butuh koordinat aslinya.

Maka, kita definisikan Fungsi Kernel $K(x_i,x_j)$ yang bisa langsung menghitung hasil dot product di dimensi tinggi TANPA kita perlu tahu bentuk transformasi $\varphi (x)$-nya.

$K(x_i,x_j)=\varphi (x_i)\cdot \varphi (x_j)$

Jadi,

$f(x)={\sum }_{i=1}^{ns}{\alpha }_i{y}_{i}K(x_i,x)+b$

6. Jenis-Jenis Kernel Populer

Kernel	Rumus Matematika	Karakteristik
Linear	$K(x,z)=x^{T}z$	Sama seperti SVM biasa. Cepat. Bagus untuk data teks/dimensi sangat tinggi.
Polynomial	$K(x,z)=(x^{T}z+r{)}^d$	Membentuk batas melengkung polinomial. Parameter $d$ (derajat) menentukan kompleksitas.
RBF (Gaussian)	$K(x,z)=\exp (-\gamma \Vert x_i-x_j{\Vert }^2)$	-
Sigmoid	$K(x,z)=\tanh (\gamma x^{T}z+r)$	Mirip perilaku Neural Network.

Panduan Pemilihan Kernel SVM

1. Linear Kernel

Formula:

$K(x_i,x_j)=x_i\cdot x_j$

Kapan Digunakan:

✅ Data Linearly Separable

• Data sudah bisa dipisahkan dengan garis/bidang lurus
• Tidak perlu transformasi ke dimensi lebih tinggi

✅ Dimensi Tinggi, Data Sedikit

• Text classification (bag-of-words: 10,000+ fitur)
• Gene expression data (ribuan gen, ratusan sampel)
• Spam detection

✅ Dataset Besar

• Linear kernel paling cepat!
• Kompleksitas: O(n × d) dimana n = data, d = dimensi
• Cocok untuk jutaan data

✅ Butuh Interpretasi Model

• Koefisien w bisa diinterpretasi (feature importance)
• Tidak ada “black box” dari transformasi kernel

Contoh Kasus:

• Spam detection: Email dengan 50,000 kata unik → sudah high-dimensional
• Document classification: TF-IDF vectors
• Sentiment analysis: Text features

Kelebihan:

• ⚡ Sangat cepat
• 💾 Hemat memori
• 📊 Mudah diinterpretasi
• 🎯 Tidak ada hyperparameter kernel

Kekurangan:

• ❌ Tidak bisa handle non-linear patterns
• ❌ Performa buruk jika data not separable

---

2. Polynomial Kernel

Formula:

$K(x_i,x_j)=(x_i\cdot x_j+c{)}^d$

Hyperparameters:

• d (degree): Derajat polynomial (biasanya 2-5)
• c (coef0): Konstanta (biasanya 0 atau 1)

Kapan Digunakan:

✅ Data dengan Hubungan Polynomial

• Feature interactions penting
• Contoh: Hubungan kuadratik antara fitur

✅ Image Processing

• Pixel intensity relationships
• Texture classification
• Computer vision tasks

✅ Masalah dengan Batas Non-Linear Smooth

• Boundary yang melengkung tapi tidak terlalu kompleks
• Lebih “global” daripada RBF

Degree yang Umum:

d = 2 (Quadratic):

• Menangkap interaksi pasangan fitur
• Boundary berbentuk parabola, elips, hiperbola
• Paling umum digunakan

d = 3 (Cubic):

• Menangkap interaksi lebih kompleks
• Boundary lebih fleksibel

d > 3:

• Jarang digunakan (overfitting!)
• Komputasi mahal

Contoh Kasus:

• Image recognition: Pixel relationships
• Bioinformatics: Protein structure prediction
• Natural Language Processing: N-gram interactions

Kelebihan:

• ✓ Menangkap feature interactions
• ✓ Lebih global daripada RBF
• ✓ Boundary lebih smooth

Kekurangan:

• ⚠️ Sensitif terhadap d (degree)
• ⚠️ Nilai K bisa sangat besar (numerical instability)
• 🐌 Lebih lambat dari linear
• 📈 Risk overfitting jika d terlalu besar

---

3. RBF (Radial Basis Function) / Gaussian Kernel

Formula:

$K(x_i,x_j)=\exp \left(-\gamma ||x_i-x_j|{|}^2\right)$

Hyperparameter:

• γ (gamma): Kontrol “reach” dari training samples
  • γ besar → Decision boundary lebih kompleks (lokal)
  • γ kecil → Decision boundary lebih smooth (global)

Kapan Digunakan:

✅ Data Non-Linear Kompleks

• Tidak tahu pola pastinya
• Boundary sangat tidak teratur
• Default choice untuk kebanyakan masalah!

✅ Dimensi Rendah-Sedang

• Fitur < 1000
• Data tidak terlalu sparse

✅ Data dengan Cluster

• Kelas membentuk kelompok-kelompok
• XOR problem, concentric circles

✅ Tidak Tahu Kernel Mana yang Cocok

• RBF adalah safe bet!
• Universal approximator

Tuning γ:

γ terlalu besar:

• Overfitting
• Setiap titik jadi “island” sendiri
• Training accuracy tinggi, test accuracy rendah

γ terlalu kecil:

• Underfitting
• Hampir seperti linear kernel
• Tidak menangkap kompleksitas data

Contoh Kasus:

• General classification: Kebanyakan masalah real-world
• Face recognition: Non-linear facial features
• Handwritten digit recognition: MNIST
• Medical diagnosis: Complex symptom relationships
• Customer segmentation: Non-linear behavior patterns

Kelebihan:

• 🌟 Paling fleksibel
• ✓ Universal approximator (bisa fit hampir semua fungsi)
• ✓ Hanya 1 hyperparameter (γ)
• ✓ Bekerja baik untuk kebanyakan kasus

Kekurangan:

• 🐌 Lebih lambat dari linear
• 💾 Memory-intensive untuk dataset besar
• ⚠️ Sensitif terhadap γ (butuh tuning)
• 📊 Sulit interpretasi (black box)

---

4. Sigmoid Kernel

Formula:

$K(x_i,x_j)=\tanh (\gamma x_i\cdot x_j+c)$

Hyperparameters:

• γ (gamma)
• c (coef0)

Kapan Digunakan:

⚠️ Jarang Digunakan dalam Praktik!

✅ Neural Network Approximation

• Ingin efek mirip 2-layer neural network
• Historical interest (SVM as NN)

✅ Specific Research Problems

• Beberapa paper lama menggunakannya
• Bioinformatics (certain protein kernels)

Masalah Sigmoid Kernel:

❌ Tidak Selalu Positive Definite

• Bisa melanggar Mercer’s theorem
• Optimasi tidak dijamin konvergen

❌ Sulit Tuning

• 2 hyperparameters (γ dan c)
• Sangat sensitif terhadap nilai keduanya

❌ Performa Inconsistent

• Sering kalah dari RBF
• Tidak ada keuntungan jelas

Rekomendasi:

🚫 Hampir selalu lebih baik pakai RBF atau Polynomial

---

Decision Tree: Pilih Kernel Mana?

START
  ↓
Sudah tahu data linearly separable?
  ├─ Ya → LINEAR KERNEL ✓
  └─ Tidak tahu/Non-linear
       ↓
     Dimensi data?
       ├─ Sangat tinggi (>10,000 fitur)
       │    ├─ Data sparse (text/NLP) → LINEAR KERNEL ✓
       │    └─ Data dense → RBF atau LINEAR
       │
       ├─ Rendah-Sedang (<1,000 fitur)
       │    ↓
       │  Punya domain knowledge tentang pola?
       │    ├─ Ya, hubungan polynomial → POLYNOMIAL (d=2 atau 3)
       │    ├─ Ya, cluster/non-linear kompleks → RBF ✓
       │    └─ Tidak tahu → RBF ✓ (safe default)
       │
       └─ Dataset sangat besar (jutaan data)?
            └─ LINEAR KERNEL ✓ (efficiency)

---

Perbandingan Praktis

Kernel	Speed	Flexibility	Interpretability	Tuning Difficulty	Best For
Linear	⚡⚡⚡⚡⚡	⭐	📊📊📊📊	✓✓✓✓ (none)	High-dim, text, large data
Polynomial	⚡⚡⚡	⭐⭐⭐	📊📊	✓✓ (medium)	Image, interactions
RBF	⚡⚡	⭐⭐⭐⭐⭐	📊	✓✓✓ (1 param)	General non-linear, default
Sigmoid	⚡⚡	⭐⭐	📊	✓ (hard)	❌ Avoid

---

Real-World Examples

Text Classification (Spam Detection)

Features: 50,000 (bag-of-words)
Data: 100,000 emails
✓ Kernel: LINEAR (fast, interpretable)

Face Recognition

Features: 128 (face embeddings)
Data: 10,000 faces
✓ Kernel: RBF (non-linear facial features)

Medical Diagnosis

Features: 20 (blood test results)
Data: 5,000 patients
✓ Kernel: RBF (complex relationships)

Image Classification (CIFAR-10)

Features: 3072 (32×32×3 pixels)
Data: 60,000 images
✓ Kernel: RBF atau Polynomial
(But use CNN instead! 😉)

---

TL;DR - Quick Guide

Use LINEAR if:

• ✓ High-dimensional data (text, genes)
• ✓ Large dataset (millions of points)
• ✓ Need speed & interpretability
• ✓ Budget 1 jam training ⏰

Use RBF if:

• ✓ Non-linear data (don’t know pattern)
• ✓ Medium-sized dataset
• ✓ Default choice when unsure
• ✓ Budget 1 hari training 📅

Use POLYNOMIAL if:

• ✓ Know there are feature interactions
• ✓ Image/computer vision
• ✓ Prefer global boundary over local

Use SIGMOID:

• ❌ Rarely! Consider RBF instead

Golden Rule: Start Linear → Try RBF → Tune → Consider Polynomial if needed

🎯 90% of time: LINEAR or RBF is enough!

Summary

Untuk menangani data yang tidak terpisah linear, SVM menggunakan dua pendekatan utama: Soft Margin dan Kernel Trick. Soft Margin menggunakan Slack Variables ($\xi$) untuk mentoleransi noise, dikontrol oleh parameter C (Regularisasi). Kernel Trick memungkinkan SVM memisahkan data dengan pola non-linear kompleks dengan cara memproyeksikan data ke dimensi tinggi secara implisit, menghindari beban komputasi transformasi manual. Kernel populer termasuk Polynomial dan RBF.

Ad Libitum: Detail Matematis Kernel

1. Formulasi Dual dengan Slack Variables

Menariknya, ketika kita menambahkan slack variable, bentuk persamaan Dual Problem tidak berubah drastis.

Persamaan Dual tetap:

$Maximize:\sum {\alpha }_i-\frac{1}{2}\sum \sum {\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i,x_j)$

Perbedaannya hanya pada kendala nilai Alpha ($\alpha$):

• Hard Margin (Linear sempurna): $0\le {\alpha }_i$

• Soft Margin (Dengan Slack): $0\le {\alpha }_i\le C$

Ini membatasi pengaruh satu data outlier agar tidak merusak model sepenuhnya (nilai $\alpha$ tidak bisa meledak sampai tak hingga).

2. Contoh Perhitungan Kernel Polinomial (Slide 50)

Misal data 1D: $x=\{1,2,4,5,6\}$ dengan label $y=\{1,1,-1,-1,1\}$.

Menggunakan Kernel Polinomial derajat 2: $K(x,y)=(xy+1{)}^2$.

Alih-alih menghitung koordinat baru, kita hitung matriks kernel antar semua titik.

Misal $K(1,2)=(1\cdot 2+1{)}^2=9$.

Setelah dimasukkan ke QP Solver, didapat Support Vectors di $x=\{2,5,6\}$.

Fungsi keputusan akhirnya menjadi persamaan kuadrat (parabola) yang memisahkan data tersebut.

Spaced Repetition Questions (Review)

1. Apa fungsi dari Slack Variable dalam SVM?

Slack Variable ($\xi$) berfungsi untuk mengukur seberapa jauh sebuah titik data melanggar margin atau salah diklasifikasikan, memungkinkan SVM untuk menemukan hyperplane meskipun data tidak terpisah sempurna (Soft Margin).

2. Jika model SVM Anda mengalami Overfitting, bagaimana sebaiknya Anda mengubah nilai parameter C?

Anda harus mengecilkan nilai C. Nilai C yang besar memaksa model untuk tidak membuat kesalahan sama sekali pada data latih (sangat ketat), yang menyebabkan margin sempit dan sensitif terhadap noise (overfitting).

3. Jelaskan konsep "Kernel Trick" dalam satu kalimat!

Metode menghitung dot product data di dimensi tinggi menggunakan fungsi kernel $K(x_i,x_j)$ tanpa perlu melakukan transformasi koordinat data secara eksplisit, sehingga menghemat komputasi.

4. Sebutkan dua jenis Kernel yang paling umum digunakan selain Linear Kernel!

1. Polynomial Kernel

2. Radial Basis Function (RBF) Kernel / Gaussian Kernel

5. Apa bedanya batasan nilai Alpha pada Soft Margin vs Hard Margin?

Pada Hard Margin, ${\alpha }_i\ge 0$ (tanpa batas atas). Pada Soft Margin, $0\le {\alpha }_i\le C$. Nilai C membatasi seberapa besar pengaruh satu data outlier terhadap model.

6. Mengapa kita menggunakan Kernel Trick daripada mentransformasi data secara manual?

Karena transformasi manual ke dimensi tinggi sangat boros memori dan komputasi (Curse of Dimensionality). Kernel Trick memungkinkan kita mendapatkan hasil yang sama (dot product di dimensi tinggi) hanya dengan operasi matematika sederhana di dimensi rendah.

7. Jika model SVM Anda terlalu kaku (Underfitting) pada data pelatihan, parameter apa yang harus diubah?

Anda bisa mencoba menaikkan nilai C (agar model lebih ketat/sedikit toleransi error) atau menaikkan nilai Gamma (jika pakai RBF, agar model lebih sensitif terhadap detail lokal).