IF Notes

Alpha-beta Pruning

4 min read

Back to IF3170 Inteligensi Artifisial

Topic

Questions/Cues

  • Apa itu Alpha-Beta Pruning?

  • Apa tujuan utamanya?

  • Apa itu nilai Alpha (α)?

  • Apa itu nilai Beta (β)?

  • Kapan sebuah cabang dipangkas?

  • Seberapa efektif optimisasi ini?

Reference Points

  • IF3170_Materi04-AdversarialSearch.pdf (Slide 10-17)

Alpha-Beta Search (atau Alpha-Beta Pruning) bukanlah algoritma baru, melainkan sebuah optimisasi untuk algoritma Minimax. Tujuannya adalah untuk mengurangi jumlah simpul (nodes) yang perlu dievaluasi dalam game tree secara drastis.

Ide utamanya adalah: “Jika kita sudah menemukan sebuah langkah yang bagus, kita tidak perlu membuang waktu mengevaluasi langkah lain yang kita tahu pasti akan lebih buruk.” Algoritma ini “memangkas” (prunes) cabang-cabang dari game tree yang tidak akan mungkin mempengaruhi keputusan akhir. Hebatnya, hasil keputusan akhir akan selalu sama persis dengan Minimax standar.

Cara Kerja: Nilai Alpha (α) dan Beta (β)

Algoritma ini bekerja dengan melacak dua nilai selama proses penelusuran (depth-first search):

  1. Alpha (α):
    • Mewakili nilai terbaik (tertinggi) yang bisa dijamin oleh MAX sejauh ini, di sepanjang path dari akar.
    • Dimulai dari .
    • Nilai α hanya bisa diperbarui di level MAX.
  2. Beta (β):
    • Mewakili nilai terbaik (terendah) yang bisa dijamin oleh MIN sejauh ini, di sepanjang path dari akar.
    • Dimulai dari .
    • Nilai β hanya bisa diperbarui di level MIN.

Kondisi Pruning

Pemangkasan (pruning) terjadi pada sebuah simpul ketika α ≥ β.

  • Logikanya: Misalkan kita berada di sebuah simpul MIN. Jika nilai Beta (pilihan terbaik MIN saat ini, yaitu nilai terendah) sudah lebih kecil dari atau sama dengan nilai Alpha (jaminan nilai terbaik MAX di cabang lain), maka tidak ada gunanya melanjutkan penelusuran di cabang ini. Mengapa? Karena MAX sudah memiliki opsi lain (yang menghasilkan nilai α) yang lebih baik daripada apa pun yang bisa ditawarkan oleh cabang saat ini (yang terbaiknya saja hanya β). MAX tidak akan pernah memilih jalur ini.

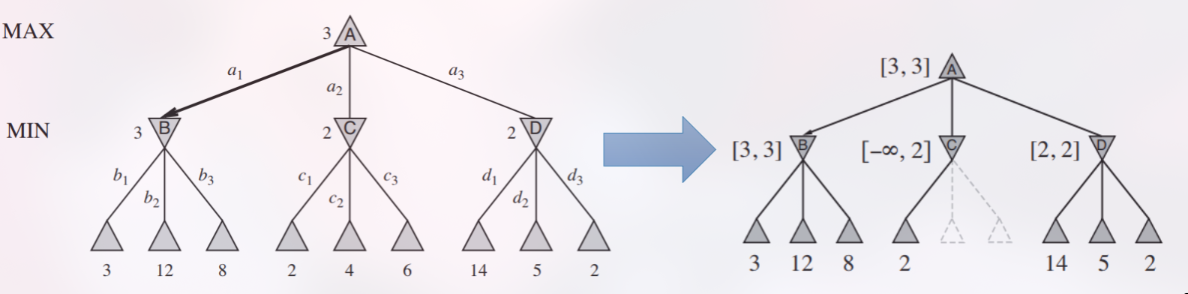
Contoh dari slide: Setelah mengevaluasi cabang B, MAX tahu ia bisa mendapatkan skor minimal 3 (α = 3). Kemudian saat mengevaluasi cabang C, MIN menemukan langkah dengan nilai 2. Pada titik ini, nilai pada simpul C dijamin akan ≤ 2 (β = 2). Karena α (3) ≥ β (2), sisa anak dari C tidak perlu dievaluasi. MAX tidak akan pernah memilih cabang C karena sudah ada cabang B yang lebih baik.

Efektivitas Alpha-Beta Pruning

Efektivitas pruning sangat bergantung pada urutan evaluasi langkah (move ordering).

  • Kasus Terbaik: Jika langkah-langkah terbaik selalu dievaluasi terlebih dahulu, kompleksitas waktu dapat berkurang dari O(bm) menjadi O(bm/2). Ini adalah peningkatan eksponensial, yang berarti kita bisa mencari dua kali lebih dalam dengan jumlah waktu yang sama.

  • Kasus Terburuk: Jika langkah dievaluasi dalam urutan terburuk, tidak ada cabang yang akan dipangkas sama sekali, dan performanya akan sama dengan Minimax standar.

Summary

Alpha-Beta Search adalah sebuah optimisasi cerdas untuk Minimax yang secara signifikan mengurangi kompleksitas komputasi tanpa mengubah hasil akhir. Ini dicapai dengan melacak dua nilai, Alpha (jaminan skor terbaik untuk MAX) dan Beta (jaminan skor terbaik untuk MIN), dan memangkas (pruning) cabang-cabang dalam game tree ketika kondisi α ≥ β terpenuhi, karena cabang tersebut terbukti tidak akan mempengaruhi keputusan optimal.

Graph View

Backlinks