Pengantar Adversarial Search

Back to IF3170 Inteligensi Artifisial

Topic

Questions/Cues

• Apa itu Pencarian Adversarial?

• Bedanya dengan pencarian biasa?

• Apa saja komponen formalnya?

• Bagaimana game direpresentasikan?

• Apa itu fungsi utilitas?

Reference Points

• IF3170_Materi04-AdversarialSearch.pdf (Slide 2-5)

Definisi Pencarian Adversarial

Pencarian Adversarial adalah sebuah metode pencarian yang digunakan dalam lingkungan multi-agen yang kompetitif, di mana tujuan satu agen berlawanan langsung dengan tujuan agen lain. Lingkungan ini sering disebut sebagai “permainan” (games).

Berbeda dengan pencarian non-adversarial (seperti A* atau BFS) yang tujuannya adalah menemukan jalur optimal ke sebuah goal state, tujuan dari pencarian adversarial adalah untuk menemukan strategi atau kebijakan (policy) yang akan membawa agen ke kemenangan, dengan asumsi lawan juga bermain secara optimal untuk menang.

Karakteristik utama dari game yang dibahas di sini adalah:

• Deterministik: Tidak ada elemen acak (seperti lemparan dadu).

• Turn-taking: Pemain bergerak secara bergiliran.

• Informasi Sempurna (Fully Observable): Semua pemain dapat melihat seluruh state permainan (misalnya, papan catur terlihat oleh kedua pemain).

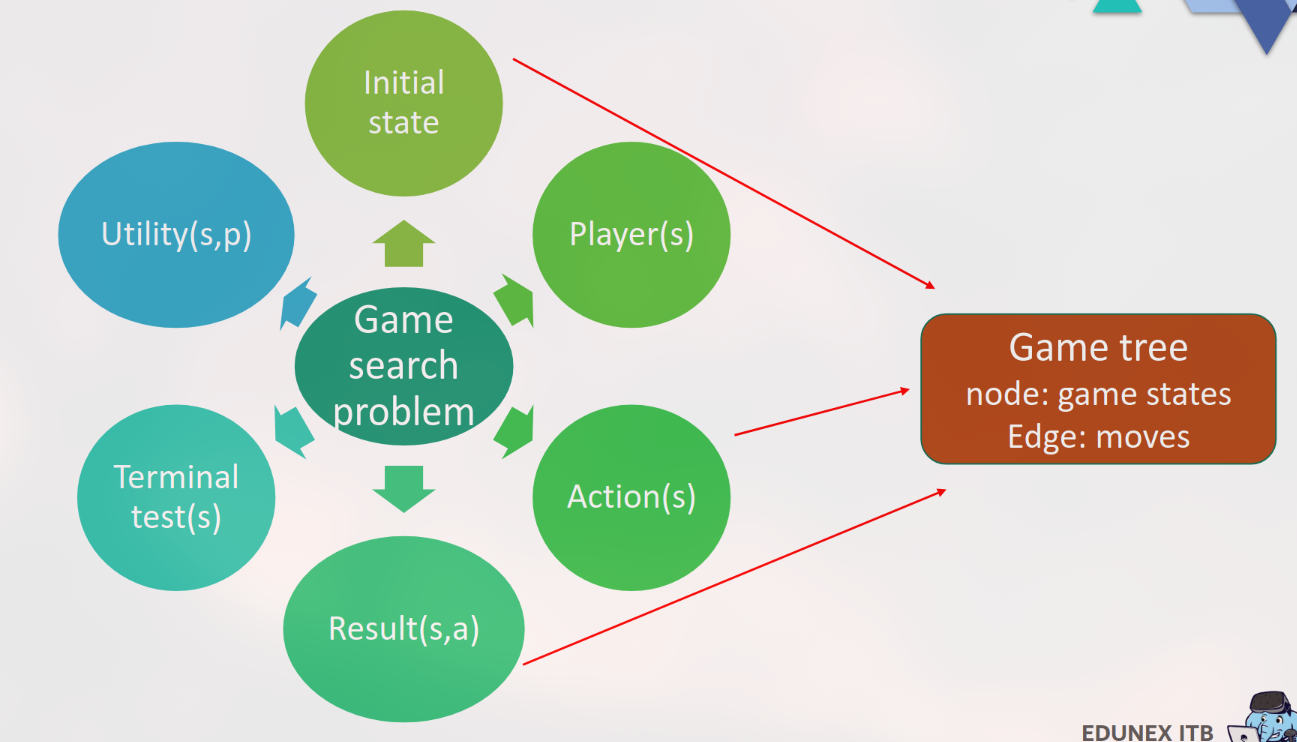
Komponen Formal Masalah Game Search

Sebuah masalah pencarian dalam game dapat didefinisikan secara formal dengan beberapa komponen:

1. Initial State: Konfigurasi awal permainan saat dimulai.

2. Player(s): Menentukan pemain mana yang akan bergerak pada state tertentu.

3. Action(s)(s): Kumpulan langkah (moves) yang legal dari sebuah state s.

4. Result(s, a): State transisi yang dihasilkan setelah pemain melakukan aksi a dari state s.

5. Terminal Test(s): Sebuah fungsi yang menentukan apakah permainan telah berakhir (menang, kalah, atau seri). State di mana permainan berakhir disebut terminal state.

6. Utility(s, p): Sebuah fungsi yang memberikan nilai numerik (skor) untuk pemain p pada terminal state s. Nilai ini merepresentasikan hasil akhir dari permainan. Sebagai contoh:

• +1: Pemain p menang.

• -1: Pemain p kalah.

• 0: Permainan berakhir seri.

Representasi Game: Game Tree

Seluruh kemungkinan jalannya sebuah permainan dapat direpresentasikan menggunakan sebuah struktur data yang disebut Game Tree (Pohon Permainan).

• Nodes (Simpul): Merepresentasikan state atau konfigurasi permainan. Simpul akar (root) adalah initial state.

• Edges (Sisi): Merepresentasikan langkah atau aksi (moves) yang mungkin dari satu state ke state lainnya.

• Leaves (Daun): Merepresentasikan terminal states, yaitu akhir dari permainan. Setiap daun memiliki nilai utilitas yang terkait dengannya.

Dalam permainan dua pemain seperti catur atau tic-tac-toe, kita sering menamai pemain sebagai MAX dan MIN. MAX adalah pemain yang berusaha memaksimalkan skor utilitas, sementara MIN berusaha meminimalkan skor utilitas. Level-level pada game tree akan bergantian antara giliran MAX dan MIN.

Summary

Pencarian Adversarial adalah sebuah pendekatan untuk pengambilan keputusan dalam lingkungan kompetitif (game) dengan merepresentasikannya sebagai sebuah Game Tree, di mana setiap simpul adalah keadaan permainan dan setiap sisi adalah langkah yang mungkin. Tujuannya bukan untuk mencari path, melainkan untuk menentukan strategi optimal dengan menganalisis hasil akhir permainan (terminal states) yang memiliki nilai utilitas, dengan asumsi bahwa lawan juga akan selalu mengambil langkah terbaik untuk kepentingannya sendiri.

Additional Information

Tipe-Tipe Game Lainnya

Materi ini berfokus pada game deterministik dengan informasi sempurna. Namun, ada juga tipe game lain yang memerlukan pendekatan berbeda:

• Game dengan Elemen Acak (Stochastic Games): Seperti backgammon atau monopoli, di mana ada lemparan dadu. Ini memerlukan algoritma seperti Expectiminimax.

• Game dengan Informasi Tidak Sempurna (Imperfect Information Games): Seperti poker atau Scrabble, di mana pemain tidak bisa melihat semua informasi (misalnya, kartu di tangan lawan). Ini memerlukan pemodelan belief states (keadaan keyakinan).

Kompleksitas Game Tree

Ukuran game tree bisa menjadi sangat besar. Kompleksitasnya ditentukan oleh:

• Branching Factor (b): Rata-rata jumlah langkah yang mungkin dari setiap state.

• Maximum Depth (m): Jumlah langkah maksimum dalam satu permainan.

Ukuran total game tree bisa mencapai O(bm). Untuk game seperti catur, dengan b≈35 dan m≈100, menelusuri seluruh pohon adalah hal yang mustahil. Inilah mengapa kita memerlukan algoritma yang lebih cerdas (seperti Minimax) dan teknik optimisasi (seperti Alpha-Beta Pruning).

Eksplorasi Mandiri

• Coba gambarkan game tree lengkap untuk permainan Tic-Tac-Toe yang dimulai dari papan kosong untuk 2-3 langkah pertama. Identifikasi giliran MAX dan MIN.

Sumber & Referensi Lanjutan:

• Buku: “Artificial Intelligence: A Modern Approach” oleh Stuart Russell dan Peter Norvig, Bab 5.

[!cornell] Topic

Questions/Cues

• Apa itu Adversarial Search?

• Apa karakteristik lingkungannya?

• Apa itu Game Tree?

• Siapa pemain MAX dan MIN?

• Bagaimana algoritma Minimax bekerja?

• Apa saja properti Minimax?

• Mengapa Minimax tidak praktis?

• Apa itu Alpha-Beta Pruning?

• Bagaimana Alpha-Beta Pruning bekerja?

Reference Points

• IF3170-Materi04-AdversarialSearch.pdf

Konsep Adversarial Search

Adversarial Search adalah metode pencarian yang dirancang untuk lingkungan kompetitif (multi-agen) di mana tujuan setiap agen saling bertentangan. Fokus utamanya adalah menemukan strategi atau kebijakan optimal untuk menang dalam sebuah permainan.

• Karakteristik Lingkungan:

  • Deterministik & Fully Observable: Aturan mainnya jelas dan seluruh keadaan permainan diketahui oleh semua pemain.

  • Turn-taking: Pemain bermain secara bergiliran.

  • Zero-sum: Keuntungan satu pemain adalah kerugian bagi pemain lain.

Representasi Permainan: Game Tree

Permainan direpresentasikan sebagai sebuah Game Tree, di mana:

• Node: Merepresentasikan sebuah state (konfigurasi) permainan.

• Edge: Merepresentasikan sebuah move (langkah) yang valid.

• Root: State awal permainan.

• Leaf Nodes (Terminal States): State akhir permainan (menang, kalah, atau seri), di mana setiap state ini memiliki nilai utility.

Algoritma Minimax

Minimax adalah algoritma fundamental untuk menentukan langkah optimal. Algoritma ini bekerja dengan asumsi bahwa lawan akan selalu bermain secara optimal.

• Pemain MAX: Pemain (kita) yang tujuannya memaksimalkan skor.

• Pemain MIN: Lawan yang tujuannya meminimalkan skor MAX.

• Utility Function: Fungsi yang menetapkan nilai numerik pada terminal state (misal: +1 untuk menang, -1 untuk kalah, 0 untuk seri).

Cara Kerja (Proses Backup Nilai):

1. Bangun game tree hingga ke terminal states.

2. Terapkan utility function pada setiap terminal state.

3. “Naikkan” nilai dari daun ke akar:

   • Pada level MAX, sebuah node akan mengambil nilai maksimum dari anak-anaknya.

   • Pada level MIN, sebuah node akan mengambil nilai minimum dari anak-anaknya.

4. Langkah yang dipilih MAX di awal adalah langkah yang mengarah ke anak dengan nilai tertinggi setelah proses backup.

Properti dan Keterbatasan Minimax

• Completeness: Ya, jika pohonnya terbatas.

• Optimality: Ya, jika lawan bermain secara optimal.

• Time Complexity: O(bm) (b = branching factor, m = kedalaman).

• Space Complexity: O(bm) (dengan DFS).

Keterbatasan utamanya adalah kompleksitas waktu yang eksponensial, membuatnya tidak praktis untuk game kompleks seperti catur ($b\approx 35,m\approx 100$).

Optimisasi: Alpha-Beta Pruning

Alpha-Beta Pruning adalah optimisasi cerdas dari Minimax yang dapat memangkas (prune) cabang-cabang besar dari game tree yang tidak akan memengaruhi keputusan akhir.

• Ide Utama: Berhenti mengevaluasi sebuah cabang segera setelah terbukti bahwa cabang tersebut tidak akan lebih baik dari opsi lain yang sudah ditemukan.

• Cara Kerja: Algoritma melacak dua nilai:

  • Alpha ($alpha$): Nilai terbaik (tertinggi) yang sudah dijamin untuk MAX di sepanjang path saat ini.
  • Beta ($beta$): Nilai terbaik (terendah) yang sudah dijamin untuk MIN di sepanjang path saat ini.

• Kondisi Pruning: Sebuah cabang di level MIN akan di-prune jika nilainya lebih rendah dari atau sama dengan alpha ($\le \alpha$), dan cabang di level MAX akan di-prune jika nilainya lebih tinggi dari atau sama dengan beta ($\ge \beta$). Dengan kata lain, pemangkasan terjadi ketika $\alpha \ge \beta$.

Summary

Adversarial Search digunakan untuk menemukan strategi optimal dalam permainan kompetitif dengan memodelkannya sebagai game tree. Algoritma Minimax menjadi dasarnya, dengan cara melakukan backup nilai dari akhir permainan untuk memilih langkah yang memaksimalkan keuntungan (MAX) sambil mengasumsikan lawan akan meminimalkan keuntungan tersebut (MIN). Karena Minimax memiliki kompleksitas eksponensial, optimisasi krusial seperti Alpha-Beta Pruning sangat penting untuk memangkas cabang pohon yang tidak relevan, membuat pencarian menjadi jauh lebih efisien tanpa mengubah kualitas keputusan.

Additional Information

Pencarian dengan Kedalaman Terbatas (Resource Limits)

Untuk game yang terlalu kompleks untuk dijelajahi sepenuhnya, pendekatan praktis yang digunakan adalah:

1. Cutoff Test: Menghentikan pencarian setelah kedalaman tertentu (misalnya, 10 langkah ke depan).

2. Evaluation Function: Karena pencarian tidak mencapai akhir permainan, diperlukan sebuah fungsi evaluasi heuristik untuk memperkirakan seberapa bagus sebuah posisi non-terminal. Fungsi ini biasanya merupakan kombinasi dari berbagai fitur permainan (misalnya dalam catur: material, posisi, keamanan raja).

Game dengan Elemen Acak (Stochastic Games)

Untuk permainan yang melibatkan elemen acak seperti lemparan dadu (contoh: Backgammon), game tree dimodifikasi dengan menambahkan chance nodes. Nilai yang dihitung bukanlah nilai minimax pasti, melainkan nilai harapan (expected value) dari semua kemungkinan hasil acak.

Eksplorasi Mandiri

• Coba visualisasikan proses Alpha-Beta Pruning pada pohon di slide. Lacak nilai alpha dan beta di setiap node untuk memahami mengapa cabang X di bawah node C bisa dipangkas.

• Rancang sebuah evaluation function sederhana untuk Tic-Tac-Toe. Misalnya, $E(s)=(\text{jumlahbarisXbisamenang})-(\text{jumlahbarisObisamenang})$. Bagaimana fungsi ini bisa membantu Minimax membuat keputusan bahkan sebelum mencapai akhir permainan?