Terminologi dalam CSP

Back to IF3170 Inteligensi Artifisial

Topic

Questions/Cues

• Apa itu CSP?

• Apa 3 komponen formalnya?

• Bagaimana contoh CSP?

• Bagaimana CSP divisualisasikan?

• Apa saja variasi variabel?

• Apa saja jenis constraint?

Reference Points

• IF3170_Materi04_AI-CSP.pdf (Slide 1-6)

Definisi Constraint Satisfaction Problem (CSP)

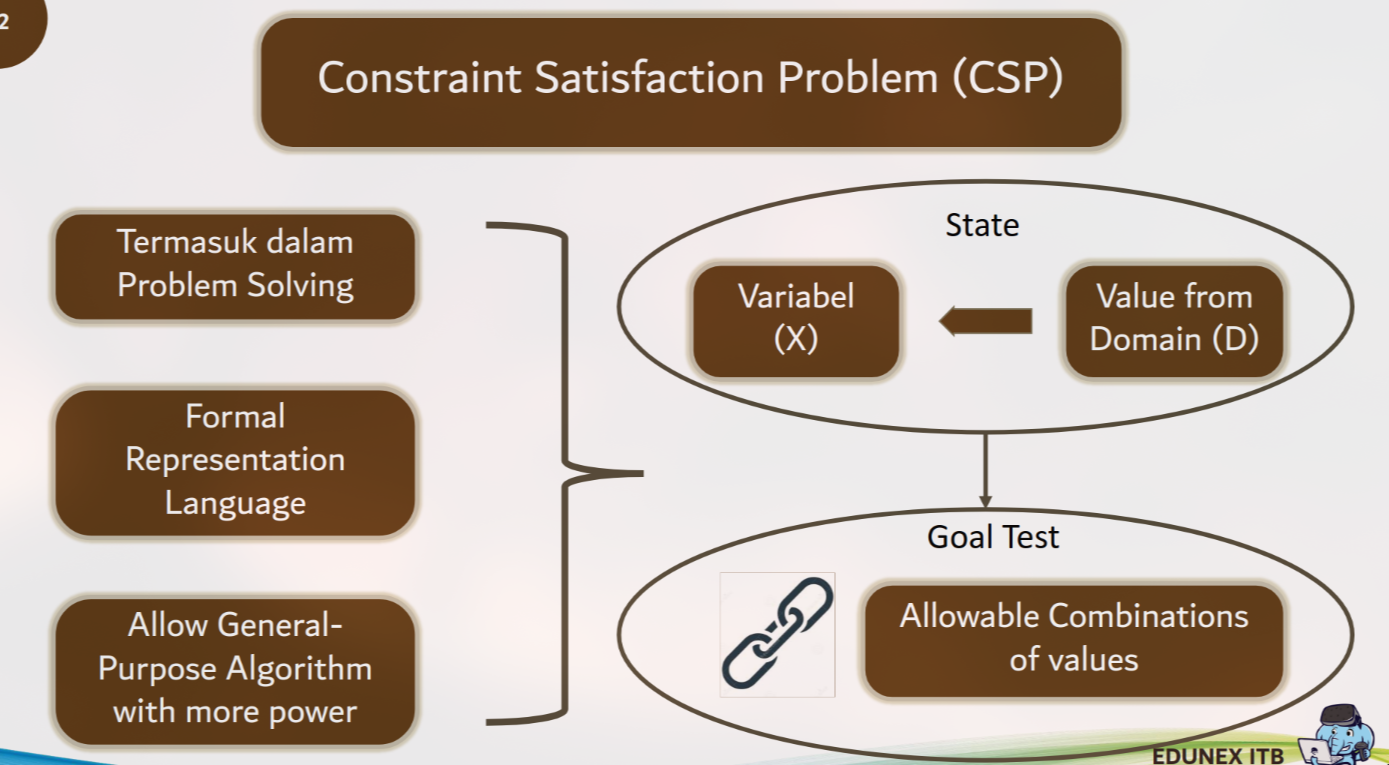
CSP adalah sebuah kerangka kerja (framework) yang kuat untuk menyelesaikan masalah dengan merepresentasikannya secara formal. Ini memungkinkan penggunaan algoritma serbaguna untuk menemukan solusi.

Secara konseptual, sebuah CSP didefinisikan oleh:

• State: Didefinisikan oleh variabel (X) yang diberi nilai (value) dari sebuah domain (D).

• Goal Test: Memeriksa apakah kombinasi nilai yang diberikan kepada variabel memenuhi semua constraints (aturan/batasan) yang ada.

Solusi dari sebuah CSP adalah sebuah assignment (penugasan nilai) yang lengkap (semua variabel punya nilai) dan konsisten (tidak melanggar constraint).

Komponen Formal CSP

Sebuah CSP secara formal terdiri dari tiga komponen utama:

1. X (Variables): Sebuah himpunan variabel $\{X_1,X_2,...,X_n\}$ yang perlu dicarikan nilainya.

2. D (Domain): Sebuah himpunan domain $\{D_1,D_2,...,D_n\}$, di mana setiap Di​ berisi kumpulan nilai yang mungkin untuk variabel $X_i$​.

3. C (Constraints): Sebuah himpunan constraints yang menentukan kombinasi nilai yang diperbolehkan untuk variabel-variabel yang saling terkait.

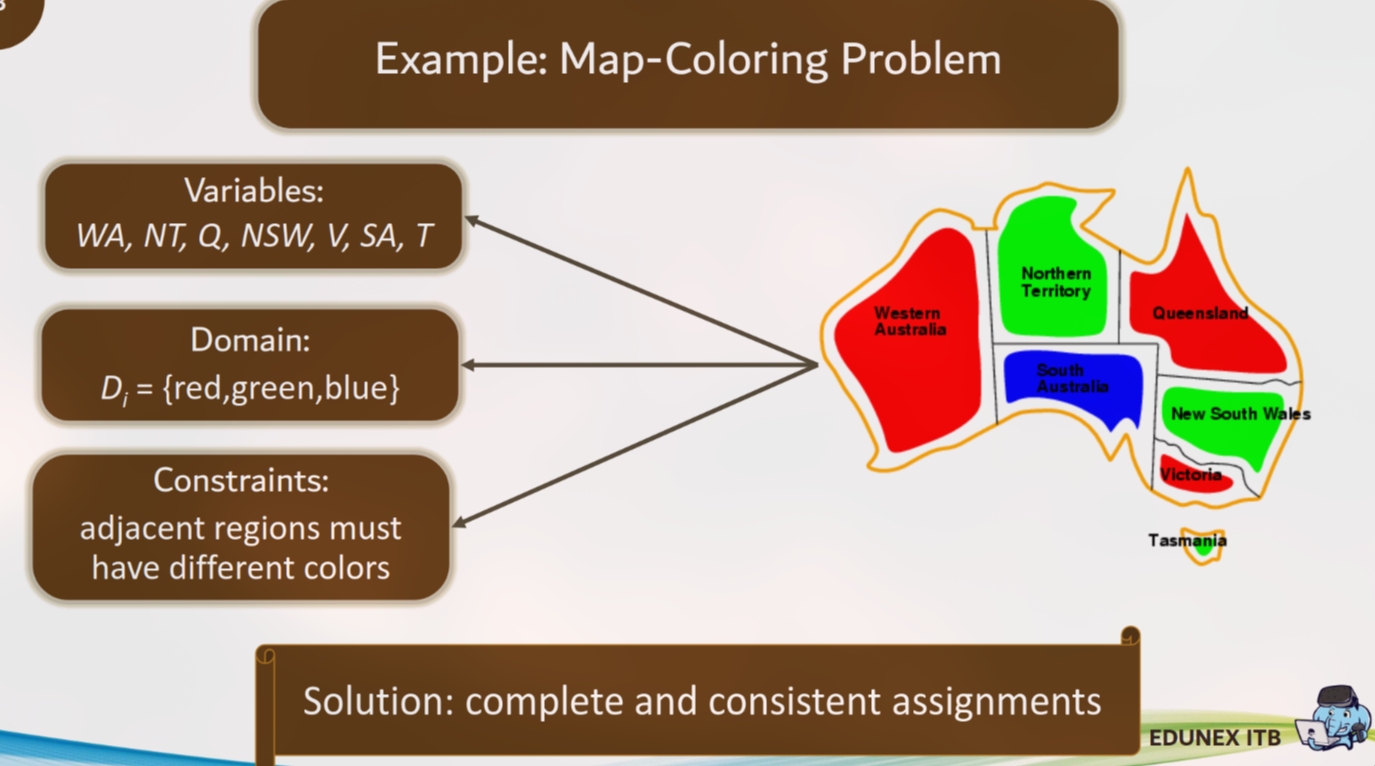
Contoh: Masalah Pewarnaan Peta (Map Coloring)

• Variables (X): Wilayah pada peta, misal: {WA,NT,Q,NSW,V,SA,T}.

• Domain (D): Warna yang bisa digunakan, misal: Di​={merah,hijau,biru}.

• Constraints (C): Wilayah yang bertetangga harus memiliki warna yang berbeda. Contoh: WA $\ne$ NT.

Visualisasi CSP

Masalah CSP dapat divisualisasikan dalam bentuk graf:

• Constraint Graph: Representasi sederhana di mana variabel menjadi nodes (simpul) dan binary constraints (batasan antara dua variabel) menjadi links/arcs (sisi).

• Constraint Hypergraph: Digunakan ketika terdapat higher-order constraints (batasan yang melibatkan lebih dari dua variabel). Constraint ini direpresentasikan sebagai “kotak” atau kontainer yang menghubungkan semua variabel yang terlibat.

Variasi dalam Formalisme CSP

1. Berdasarkan Variabel:

• Discrete: Domain memiliki jumlah nilai yang bisa dihitung.

  • Finite Domain: Jumlah nilai terbatas (misal: warna, booleans). Ini adalah jenis CSP yang paling umum dipelajari.

  • Infinite Domain: Jumlah nilai tidak terbatas (misal: bilangan bulat untuk penjadwalan). Memerlukan constraint language khusus, contoh: StartJob1​+5≤StartJob2​.

• Continuous: Domain memiliki nilai dari rentang kontinu (misal: bilangan real). Sering diselesaikan dengan metode linear/quadratic programming.

2. Berdasarkan Constraints:

• Unary: Batasan pada satu variabel. Contoh: SA $\ne$ hijau.

• Binary: Batasan antara dua variabel. Contoh: SA $\ne$ WA.

• Higher-Order: Batasan yang melibatkan tiga atau lebih variabel. Contoh: Constraint pada masalah Cryptarithmetic (seperti TWO + TWO = FOUR).

• Preference (Soft Constraints): Bukan batasan mutlak, melainkan preferensi. Ini mengarah ke Constraint Optimization Problem (COP), di mana tujuannya adalah mencari solusi terbaik, bukan sekadar solusi yang valid.

Summary

Constraint Satisfaction Problem (CSP) adalah sebuah metode formal untuk merepresentasikan masalah sebagai satu set variabel yang harus diberi nilai dari domain tertentu, dengan mematuhi serangkaian batasan (constraints). Solusi yang dicari adalah penugasan nilai yang lengkap dan konsisten. Variasi dalam tipe variabel (discrete/continuous) dan constraint (unary/binary/higher-order) memungkinkan CSP untuk memodelkan berbagai macam masalah di dunia nyata.

Additional Information

Kekuatan Abstraksi CSP

Keindahan CSP terletak pada kemampuannya untuk mengabstraksi masalah. Kita tidak perlu membuat algoritma spesifik untuk Sudoku, algoritma lain untuk penjadwalan kelas, dan algoritma lain untuk pewarnaan peta. Selama kita bisa memformulasikan masalah-masalah tersebut ke dalam bentuk Variabel, Domain, dan Constraint, kita bisa menggunakan algoritma CSP general (seperti Backtracking atau Local Search) untuk menyelesaikannya.

Contoh Formulasi Masalah Lain

• Sudoku:

  • Variabel: 81 kotak di papan Sudoku.

  • Domain: Angka {1, 2, …, 9} untuk setiap kotak.

  • Constraints: Angka di setiap baris, kolom, dan sub-grid 3x3 harus unik (menggunakan constraint Alldiff).

• Penjadwalan Kelas:

  • Variabel: Setiap mata kuliah yang harus dijadwalkan.

  • Domain: Kombinasi {Ruangan, Waktu, Dosen}.

  • Constraints: Sebuah ruangan tidak bisa dipakai oleh dua kelas di waktu yang sama; seorang dosen tidak bisa mengajar dua kelas di waktu yang sama; sebuah kelas tidak boleh bentrok dengan kelas prasyaratnya.

Eksplorasi Mandiri

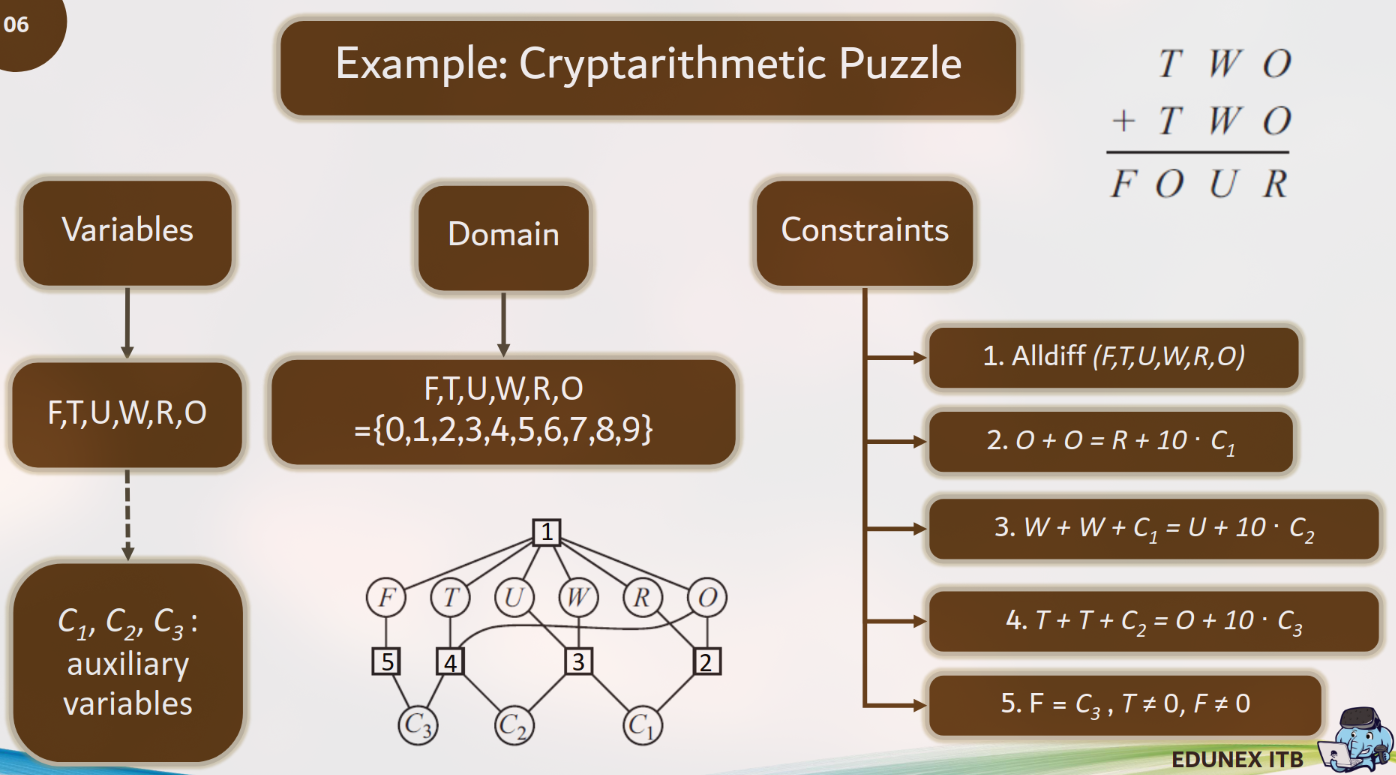
Coba pecah masalah Cryptarithmetic TWO + TWO = FOUR seperti pada slide 6. Identifikasi semua variabel (termasuk variabel bantu C1, C2, C3), domainnya, dan kelima constraint yang dijelaskan.