Pengenalan Pada Grup

Back to MA2022 Struktur Bilangan Bulat

Pengenalan Pada Grup

Questions/Cues

• Apa itu Grup?
• Apa saja Aksioma Grup?
• Apa itu Grup Abelian?
• Apa itu Tabel Cayley?
• Contoh-contoh Grup
• Kenapa (ℤ, ⋅) bukan Grup?

Catatan

Definisi Grup

Sebuah Grup adalah struktur aljabar yang terdiri dari sebuah himpunan tak kosong G yang dipasangkan dengan satu operasi biner *, yang ditulis sebagai (G, *). Operasi biner ini harus bersifat tertutup, artinya untuk setiap elemen a dan b di G, hasil dari a * b juga harus berada di dalam G.

Aksioma Grup (Syarat Wajib)

Agar (G, *) dapat disebut sebuah grup, ia wajib memenuhi tiga kondisi atau aksioma berikut:

1. Asosiatif: Urutan pengelompokan operasi tidak mengubah hasil.
   • Formal: (a * b) * c = a * (b * c) untuk semua a, b, c di G.
2. Elemen Identitas: Harus ada satu elemen spesial e di G yang jika dioperasikan dengan elemen lain, tidak akan mengubah elemen tersebut.
   • Formal: Terdapat e ∈ G sehingga a * e = e * a = a untuk semua a di G.
3. Elemen Invers: Setiap elemen di G harus memiliki “pasangan” atau invers yang jika dioperasikan akan menghasilkan elemen identitas e.
   • Formal: Untuk setiap a ∈ G, terdapat b ∈ G sehingga a * b = b * a = e.

Grup Abelian

Grup Abelian (atau Grup Komutatif) adalah jenis grup yang lebih spesifik, di mana urutan elemen dalam operasi tidak penting.

• Syarat Tambahan: Selain tiga aksioma di atas, operasi * harus bersifat komutatif.
• Formal: a * b = b * a untuk semua a, b di G.

Tabel Cayley

Tabel Cayley adalah sebuah tabel persegi yang digunakan untuk merepresentasikan operasi biner dari sebuah grup hingga. Tabel ini menyediakan cara ringkas untuk menampilkan semua kemungkinan kombinasi elemen grup dan hasilnya.

• Cara Membaca: Hasil dari a * b ditemukan pada perpotongan baris elemen a dan kolom elemen b.
• Contoh Tabel Cayley untuk (ℤ₄, +):

+ (mod 4)	0	1	2	3
0	0	1	2	3
1	1	2	3	0
2	2	3	0	1
3	3	0	1	2

• Informasi dari Tabel:
  • Tertutup: Terpenuhi jika semua entri di dalam tabel adalah anggota himpunan.
  • Identitas: 0 adalah identitas karena baris dan kolomnya sama dengan header.
  • Invers: 1⁻¹=3, 2⁻¹=2, 3⁻¹=1.
  • Abelian: Grup ini Abelian karena tabelnya simetris terhadap diagonal utama.

Contoh-contoh Grup

• (ℤ, +): Himpunan bilangan bulat dengan operasi penjumlahan. Ini adalah Grup Abelian. Identitasnya adalah 0 dan invers dari a adalah -a.
• (ℤₙ, +): Himpunan kelas residu modulo n dengan penjumlahan. Ini selalu merupakan Grup Abelian.
• (GL₂(ℝ), ⋅): Himpunan matriks 2x2 yang dapat dibalik (determinan ≠ 0) dengan perkalian matriks. Ini adalah Grup, tetapi bukan Abelian.

Kenapa (ℤ, ⋅) Bukan Grup?

Himpunan bilangan bulat dengan perkalian bukanlah sebuah grup. Walaupun ia memiliki sifat tertutup, asosiatif, dan elemen identitas (1), ia gagal pada aksioma ketiga:

• Tidak semua elemen punya invers: Sebagian besar elemen tidak memiliki invers yang merupakan bilangan bulat. Contohnya, untuk elemen 2 ∈ ℤ, tidak ada bilangan bulat b yang memenuhi 2 ⋅ b = 1.

Summary

Sebuah Grup adalah struktur aljabar fundamental yang terdiri dari sebuah himpunan tak-kosong dan satu operasi biner yang memenuhi aksioma tertutup, asosiatif, memiliki elemen identitas, dan setiap elemennya memiliki invers. Tabel Cayley dapat digunakan untuk memvisualisasikan struktur grup hingga. Jika operasi grup juga bersifat komutatif, maka grup tersebut disebut Grup Abelian. Contoh paling umum adalah (ℤ, +), sementara (ℤ, ⋅) gagal menjadi grup karena mayoritas elemennya tidak memiliki invers perkalian.

Additional Information & Contoh Soal

Informasi Tambahan

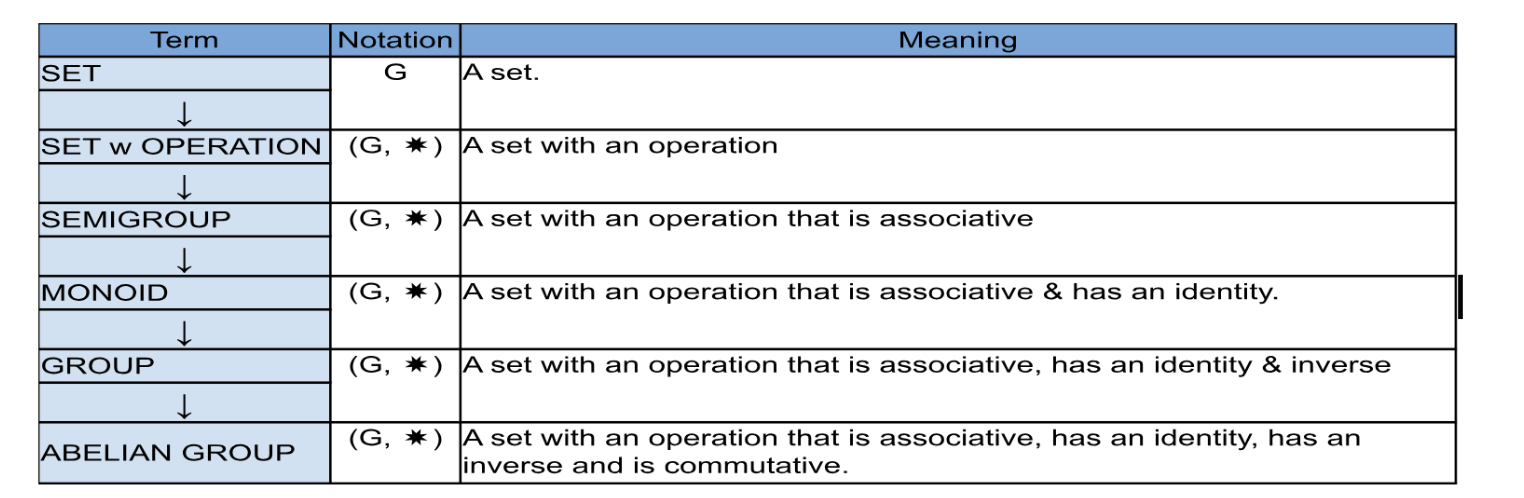
• Hierarki Struktur: Sebelum menjadi Grup, sebuah struktur dapat berupa Semigrup (hanya asosiatif) atau Monoid (asosiatif dan punya identitas). Grup menambahkan syarat wajib adanya invers untuk setiap elemen.
• Grup Hingga vs. Tak Hingga: Grup disebut hingga jika jumlah elemen di dalamnya berhingga (misalnya (ℤ₄, +)), dan tak hingga jika sebaliknya (misalnya (ℤ, +)).

Contoh Soal

1. Soal Identifikasi: Apakah himpunan bilangan asli ℕ = {1, 2, 3, ...} dengan operasi penjumlahan (+) membentuk sebuah grup?
   • Jawaban: Tidak. Operasi + pada ℕ memang asosiatif, tetapi gagal pada dua aksioma:
     • Tidak ada elemen identitas: Elemen identitas untuk penjumlahan adalah 0, tetapi 0 ∉ ℕ.
     • Tidak ada elemen invers: Bahkan jika 0 ada, tidak ada invers. Contohnya, untuk 3 ∈ ℕ, tidak ada b ∈ ℕ sehingga 3 + b = 0.
2. Soal Verifikasi: Tunjukkan bahwa U(5) adalah grup di bawah perkalian modulo 5. Apakah ia Abelian?
   • Jawaban: U(5) = {a | 1 ≤ a < 5, (a, 5) = 1} = {1, 2, 3, 4}.
   • Tabel Cayley untuk (U(5), ⋅):

⋅	1	2	3	4
1	1	2	3	4
2	2	4	1	3
3	3	1	4	2
4	4	3	2	1

- **Tertutup:** Semua hasil di dalam tabel adalah anggota `{1, 2, 3, 4}`. ✔️
- **Asosiatif:** Perkalian modulo selalu asosiatif. ✔️
- **Identitas:** Elemen `1` bertindak sebagai identitas. ✔️
- **Invers:** `1⁻¹=1`, `2⁻¹=3`, `3⁻¹=2`, `4⁻¹=4`. Semua elemen punya invers. ✔️
- **Kesimpulan:** Ya, ini adalah grup. Karena tabelnya simetris terhadap diagonal utama, ini adalah **Grup Abelian**.

3. Soal Konseptual: Kenapa himpunan matriks 2x2 dengan entri bilangan real M₂(ℝ) dan operasi perkalian bukan grup, tetapi GL₂(ℝ) (himpunan bagiannya dengan determinan tidak nol) adalah grup?
   • Jawaban: M₂(ℝ) bukan grup karena tidak semua elemennya memiliki invers. Sebuah matriks hanya memiliki invers jika determinannya tidak nol. Dengan membatasi himpunan hanya pada matriks-matriks yang determinannya tidak nol (definisi dari GL₂(ℝ)), kita memastikan bahwa aksioma invers selalu terpenuhi untuk setiap elemen.