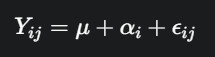ANOVA

Back to MA2281 Statistika nonparametrik

Topic

Questions/Cues

• Apa tujuan utama ANOVA?
• Apa saja asumsi yang mendasarinya?
• Bagaimana model dan hipotesis ANOVA?
• Bagaimana variabilitas data dipartisi? (SST, SSA, SSE)
• Apa itu Kuadrat Tengah (Mean Square)?
• Bagaimana mekanisme Uji-F bekerja?
• Bagaimana struktur Tabel ANOVA?
• Apa batasan dari hasil ANOVA?

Tujuan dan Konsep Dasar ANOVA

Analisis Ragam (Analysis of Variance - ANOVA) adalah sebuah prosedur statistika yang sangat kuat untuk menguji kesamaan (homogenitas) dari dua atau lebih (k>2) rerata populasi. Meskipun namanya analisis “ragam”, tujuannya adalah untuk membuat kesimpulan tentang “rerata”.

• Ide Utama: ANOVA bekerja dengan membandingkan dua sumber variasi dalam data:

  1. Variasi Antar-Kelompok (Between-Group Variation): Variasi yang disebabkan oleh perbedaan perlakuan (misalnya, jenis agregat beton yang berbeda). Ini mencerminkan efek perlakuan ditambah galat acak.

  2. Variasi Dalam-Kelompok (Within-Group Variation): Variasi yang terjadi secara acak di antara pengamatan dalam satu kelompok yang sama. Ini dianggap sebagai galat acak (random error) dan digunakan sebagai dasar perbandingan.

  • Jika variasi antar-kelompok secara signifikan lebih besar daripada variasi dalam-kelompok, kita dapat menyimpulkan bahwa perlakuan memiliki efek yang signifikan terhadap rerata.

• Asumsi Utama ANOVA Satu Arah:

  1. Independensi: Sampel yang diambil dari k populasi bersifat independen satu sama lain.
  2. Normalitas: Setiap k populasi diasumsikan berdistribusi normal.
  3. Homogenitas Ragam (Homoscedasticity): Semua k populasi memiliki ragam yang sama (σ2). Asumsi ini dapat diperiksa dengan Uji Bartlett atau Cochran.

Model, Hipotesis, dan Partisi Varians

• Model Statistik: Setiap pengamatan individual (Yij​) dapat dimodelkan sebagai:

  • μ: Rerata keseluruhan (grand mean).
  • αi​: Efek dari perlakuan ke-i.
  • ϵij​: Galat acak.

• Hipotesis:

  • H0​: Semua rerata populasi perlakuan adalah sama (μ1​=μ2​=⋯=μk​) atau, ekuivalennya, semua efek perlakuan adalah nol (α1​=α2​=⋯=αk​=0).
  • H1​: Setidaknya ada dua rerata populasi yang tidak sama.

• Partisi Jumlah Kuadrat (Sum of Squares): Variasi total dalam data (SST) dipartisi menjadi dua komponen:

  SST=SSA+SSE

  • SST (Total Sum of Squares): Mengukur variasi total dari semua data terhadap rerata keseluruhan.
  • SSA (Treatment Sum of Squares): Mengukur variasi antar-kelompok (disebabkan oleh perlakuan).
  • SSE (Error Sum of Squares): Mengukur variasi dalam-kelompok (disebabkan oleh galat acak).

Uji-F: Prosedur dan Keputusan

Uji F adalah inti dari ANOVA untuk membandingkan variasi dan membuat keputusan.

1. Kuadrat Tengah (Mean Square - MS): Ini adalah penduga ragam, dihitung dengan membagi Jumlah Kuadrat dengan derajat kebebasannya (df).

   • Kuadrat Tengah Perlakuan (MSA): $MSA=\frac{SSA}{k-1}$​. Jika H0​ benar, MSA adalah penduga tak bias dari σ2. Jika H1​ benar, MSA akan menduga nilai yang lebih besar dari σ2.
   • Kuadrat Tengah Galat (MSE): $MSE=\frac{SSE}{N-k}$​. MSE selalu menjadi penduga tak bias dari σ2, terlepas dari H0​ benar atau salah. MSE sering disebut sebagai s2.

2. Statistik Uji-F: Dihitung sebagai rasio dari dua penduga ragam.

   $F=\frac{MSA}{MSE}$

3. Aturan Keputusan:

   • Ini adalah uji sisi kanan. Jika H0​ benar, rasio F akan mendekati 1. Jika H1​ benar, MSA akan lebih besar dari MSE, sehingga menghasilkan rasio F yang besar.
   • Kita menolak H0​ jika nilai F hitung lebih besar dari nilai F kritis dari tabel (Fhitung​>Fα​(v1​,v2​)), dengan v1​=k−1 dan v2​=N−k.

Contoh dan Tabel ANOVA

Berikut adalah ringkasan perhitungan untuk data agregat beton (Contoh 13.1), di mana k=5 kelompok, n=6 sampel/kelompok, N=30.

• Hipotesis: H0​:μ1​=μ2​=μ3​=μ4​=μ5​ vs. H1​: Setidaknya ada dua rerata yang tidak sama.
• Perhitungan: Dari data, diperoleh SSA=85,356, SSE=124,021, dan SST=209,377.
• Tabel ANOVA:

Sumber Variasi	Jumlah Kuadrat (SS)	Derajat Bebas (df)	Kuadrat Tengah (MS)	F Hitung
Perlakuan (Agregat)	85,356	4 (k−1)	21,339 (SSA/4)	4.30
Galat (Error)	124,021	25 (N−k)	4,961 (SSE/25)
Total	209,377	29 (N−1)

• Keputusan:
  • Nilai kritis untuk α=0.05 dengan v1​=4 dan v2​=25 adalah F0.05​(4,25)=2.76.
  • Karena Fhitung​=4.30>2.76, kita menolak H0​.
  • Kesimpulan: Terdapat bukti yang signifikan untuk menyimpulkan bahwa tidak semua jenis agregat memiliki rerata penyerapan air yang sama.

Batasan Hasil ANOVA

• Jika uji ANOVA menghasilkan penolakan H0​, kesimpulannya hanyalah “setidaknya ada dua rerata populasi yang berbeda”.
• ANOVA tidak memberitahu kita secara spesifik pasangan rerata mana yang berbeda. Untuk mengetahui hal ini, diperlukan analisis lanjutan yang disebut Uji Perbandingan Ganda atau Post-Hoc Test (seperti Uji Tukey, Duncan, atau Dunnett).

Summary

Analisis Ragam (ANOVA) adalah prosedur untuk menguji kesamaan rerata dari lebih dari dua kelompok dengan cara mempartisi variasi total data menjadi variasi antar-kelompok (perlakuan) dan variasi dalam-kelompok (galat). Keputusan dibuat menggunakan Uji-F, yang membandingkan rasio kedua variasi tersebut. Jika hasil ANOVA signifikan (menolak H0​), itu hanya menandakan adanya perbedaan, namun tidak merinci di mana perbedaan itu berada, sehingga memerlukan uji lanjutan (perbandingan ganda).

Additional Information (Optional)

ANOVA untuk Ukuran Sampel Tidak Sama

• Prosedur ANOVA tetap valid untuk ukuran sampel yang tidak sama (ni​). Formula untuk Jumlah Kuadrat (SS) sedikit dimodifikasi untuk mengakomodasi perbedaan ukuran ni​, dan derajat kebebasan untuk galat menjadi N−k, di mana N adalah total seluruh pengamatan.

Keuntungan Ukuran Sampel Sama

• Menggunakan ukuran sampel yang sama di setiap kelompok memiliki dua keuntungan utama:
  1. Uji-F menjadi lebih kuat (robust) atau tidak terlalu sensitif terhadap pelanggaran asumsi kesamaan ragam.
  2. Meminimalkan probabilitas terjadinya Galat Tipe II (gagal menolak H0​ yang salah).