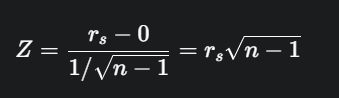Spearman

Back to MA2281 Statistika nonparametrik

Topic

Questions/Cues

• Apa definisi teknis Korelasi Spearman?
• Apa perbedaan fundamental Pearson vs. Spearman?
• Bagaimana rumus rs​ diturunkan?
• Bagaimana langkah-langkah detail perhitungannya?
• Bagaimana contoh perhitungan dengan data riil?
• Bagaimana penanganan data kembar (ties) yang benar?
• Bagaimana cara menginterpretasikan nilai rs​?
• Bagaimana prosedur lengkap uji hipotesis (sampel kecil & besar)?
• Apa saja keunggulan spesifik menggunakan rs​?

Reference Points

• Dr. Sandy Vantika - 5-Koefisien-Korelasi-Peringkat.pdf
• Walpole - Walpole - Spearman.pdf
• Kvam - Kvam - Spearman, Kendall's Tau.pdf

Konsep Fundamental dan Perbedaan Kunci

Koefisien Korelasi Peringkat Spearman (rs​) adalah ukuran asosiasi nonparametrik yang merupakan padanan dari koefisien korelasi Pearson konvensional. Disebut nonparametrik karena proses inferensinya (pengambilan kesimpulan) bebas dari asumsi distribusi populasi tertentu. Ia dihitung dengan cara mengganti nilai numerik aktual dari data dengan peringkatnya (ranks).

• Perbedaan Fundamental: Pearson vs. Spearman
  • Asumsi: Korelasi Pearson mengasumsikan bahwa data sampel diambil dari distribusi normal bivariat. Sebaliknya, Spearman tidak memerlukan asumsi normalitas sama sekali. Data hanya perlu setidaknya berada pada skala ordinal.
  • Jenis Hubungan: Pearson secara spesifik mengukur kekuatan dan arah hubungan linier (garis lurus). Spearman mengukur hubungan monotonik, yaitu hubungan di mana variabel secara konsisten bergerak ke arah yang sama (naik atau turun) tetapi tidak harus dalam garis lurus. Ini membuat Spearman lebih andal untuk data yang memiliki hubungan melengkung (kurvilinier) yang jelas.

Perhitungan Koefisien Spearman ($r_s$​)

Perhitungan rs​ didasarkan pada peringkat data, bukan nilai aslinya.

1. Formula
   • Formula Konseptual (dari Pearson): Formula Spearman secara konseptual adalah formula Pearson yang diterapkan pada peringkat ui​=rank(xi​) dan vi​=rank(yi)
   • Formula Praktis (Sederhana): Jika tidak ada data kembar (ties), formula di atas dapat disederhanakan secara aljabar menjadi:
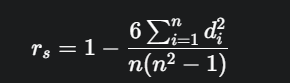
     • Di mana di​ adalah selisih antara peringkat untuk setiap pasangan data (di​=ui​−vi​).
     • n adalah jumlah pasangan data.
2. Langkah-langkah Perhitungan dan Contoh
   • Tujuan: Mengukur hubungan antara kandungan Tar dan Nikotin pada 10 merk rokok.
   • Langkah 1: Beri Peringkat pada setiap variabel secara terpisah. Peringkat 1 untuk nilai terendah, dan seterusnya.
   • Langkah 2: Tangani Data Kembar (Ties). Jika ada nilai yang sama, gunakan rata-rata dari peringkat yang seharusnya mereka tempati (disebut midranks). Pada contoh ini, merk Marlboro dan Kool sama-sama memiliki Tar 17. Mereka seharusnya menempati peringkat 4 dan 5, sehingga keduanya diberi peringkat (4+5)/2 = 4.5.
   • Langkah 3: Hitung selisih peringkat (di​) dan kuadratkan (di2​).

Cigarette Brand	Tar Content (xi​)	Nicotine Content (yi​)	Rank (xi​)	Rank (yi​)	di​	di2​
Viceroy	14	0.9	2.0	2.0	0.0	0.00
Marlboro	17	1.1	4.5	4.0	0.5	0.25
Chesterfield	28	1.6	9.0	9.0	0.0	0.00
Kool	17	1.3	4.5	6.0	-1.5	2.25
Kent	16	1.0	3.0	3.0	0.0	0.00
Raleigh	13	0.8	1.0	1.0	0.0	0.00
Old Gold	24	1.5	7.0	8.0	-1.0	1.00
Philip Morris	25	1.4	8.0	7.0	1.0	1.00
Oasis	18	1.2	6.0	5.0	1.0	1.00
Players	31	2.0	10.0	10.0	0.0	0.00
Total						5.50

• Langkah 4: Masukkan ke dalam formula.

Interpretasi dan Uji Hipotesis

Interpretasi Nilai rs​: Nilai rs​ selalu berada di antara -1 dan +1.

• +1: Asosiasi positif sempurna; peringkat kedua variabel identik.
• -1: Asosiasi negatif sempurna; peringkat kedua variabel berbanding terbalik.
• Dekat 0: Menunjukkan tidak ada korelasi atau hubungan yang sangat lemah.

Uji Hipotesis: Digunakan untuk menguji apakah ada korelasi di tingkat populasi (ρ=0).

1. Hipotesis:
   • H0​:ρ=0 (Tidak ada korelasi).
   • H1​: Bisa berupa $\rho \ne 0$ (dua arah), $\rho >0$ (satu arah, positif), atau $\rho <0$ (satu arah, negatif).
2. Prosedur Sampel Kecil (n sesuai tabel):
   • Cari nilai kritis dari Tabel A.21 berdasarkan jumlah pasangan n dan tingkat signifikansi α. Tabel ini menggunakan n, bukan derajat kebebasan.
   • Contoh Uji Hipotesis: Uji hipotesis untuk data rokok dengan α=0.01.
     • H0​:ρ=0
     • H1​:ρ>0
     • Daerah Kritis: Dari Tabel A.21 untuk n=10 dan α=0.01 (satu arah), nilai kritisnya adalah rs​>0.745.
     • Perhitungan: rs​ hitung adalah 0.967.
     • Keputusan: Karena 0.967>0.745, kita menolak H0​. Ada bukti signifikan adanya korelasi positif antara tar dan nikotin.
3. Prosedur Sampel Besar (Aproksimasi Normal):
   • Ketika n melebihi nilai di tabel (seringkali n>10 atau n>30), distribusi rs​ mendekati distribusi normal dengan rata-rata 0 dan varians 1/(n−1).​
   • Hitung z
   • Bandingkan nilai Z ini dengan nilai kritis dari tabel normal standar (misal, 1.645 untuk α=0.05 satu arah).

Summary

Koefisien Korelasi Peringkat Spearman (rs​) adalah ukuran nonparametrik yang andal untuk hubungan monotonik (baik linier maupun tidak), yang dihitung berdasarkan peringkat data. Karena tidak memerlukan asumsi normalitas, ia memiliki keunggulan fleksibilitas dibandingkan korelasi Pearson. Perhitungannya menggunakan formula sederhana yang melibatkan selisih peringkat (di​), dan signifikansinya dapat diuji menggunakan nilai kritis dari tabel untuk sampel kecil atau aproksimasi normal (uji-Z) untuk sampel besar.

Additional Information (Optional)

Derivasi dan Formula Lanjutan

• Derivasi Formula Sederhana: Formula praktis rs​ adalah hasil penyederhanaan aljabar dari formula konseptual (Pearson pada peringkat). Kunci penyederhanaannya adalah fakta bahwa untuk serangkaian peringkat dari 1 sampai n, rata-rata peringkatnya adalah R=(n+1)/2 dan jumlah kuadrat deviasinya adalah ∑(Ri​−R)2=n(n2−1)/12.
• Formula Koreksi untuk Data Kembar (Ties): Jika terdapat banyak data kembar, formula yang lebih akurat disarankan oleh Kvam untuk menyesuaikan perhitungan. Formula ini memasukkan faktor koreksi u′ dan v′ untuk masing-masing variabel. ρ^​′={[n(n2−1)−12u′][n(n2−1)−12v′]}1/2n(n2−1)−6∑i=1n​Di2​−6(u′+v′)​
  • Di mana u′=∑t(t2−1)/12, dan t adalah jumlah observasi dalam satu kelompok data kembar di variabel X (begitu pula untuk v′ di variabel Y).

Konteks dan Keunggulan Tambahan

• Konteks Historis: Charles Edward Spearman (1863-1945) adalah seorang psikolog Inggris yang menjadi pionir dalam statistik. Ia mengembangkan konsep ini sebagai bagian dari karyanya tentang kecerdasan umum dan analisis faktor.
• Keunggulan Spesifik:
  1. Tidak Memerlukan Hubungan Linier: Sangat berguna untuk data yang hubungannya monotonik tapi melengkung.
  2. Tidak Memerlukan Asumsi Normalitas: Dapat diterapkan pada data dari distribusi apa pun.
  3. Dapat Digunakan untuk Data Peringkat: Keunggulan terbesarnya adalah kemampuannya untuk digunakan pada data yang secara inheren bersifat peringkat, seperti hasil penilaian dari beberapa juri, untuk mengukur konsistensi mereka.