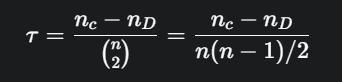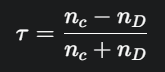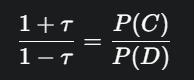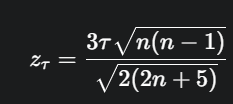Tau-Kendall

Back to MA2281 Statistika nonparametrik

Topic

Questions/Cues

• Apa itu Kendall’s Tau (τ)?
• Apa konsep pasangan Konkordan & Diskordan?
• Bagaimana formula & perhitungan τ?
• Bagaimana cara menangani data kembar (ties)?
• Bagaimana cara menginterpretasikan nilai τ?
• Apa perbedaan utama Tau Kendall dengan Spearman?
• Bagaimana prosedur uji hipotesis untuk τ?

Konsep Dasar Kendall’s Tau (τ)

Tau Kendall (τ) adalah ukuran alternatif nonparametrik untuk ketergantungan bivariat (hubungan antara dua variabel). 1 Diperkenalkan oleh Maurice George Kendall pada tahun 1938, metode ini bekerja dengan cara menghitung jumlah pasangan pengamatan yang “konkordan” dan “diskordan” dalam sebuah sampel. 2

• Pasangan Konkordan dan Diskordan
  • Konsep ini adalah inti dari Tau Kendall. Untuk setiap dua pasang pengamatan,$(Xi,Yi)$ dan $(Xj,Yj)$, kita membandingkan urutannya.
  • Pasangan Konkordan (Concordant): Pasangan yang berurutan ke arah yang sama. Artinya, jika $Xi>Xj$​, maka $Yi>Yj$​ juga. Atau jika $Xi<Xj$, maka $Yi<Yj$ juga.
  • Pasangan Diskordan (Discordant): Pasangan yang berurutan ke arah yang berlawanan. Artinya, jika $Xi>Xj$​, tetapi $Yi<Yj$. Atau sebaliknya.
  • Tujuan: Untuk mengetahui apakah secara umum pasangan dalam data cenderung konkordan (indikasi korelasi positif) atau diskordan (indikasi korelasi negatif).

Perhitungan dan Formula

Perhitungan τ didasarkan pada jumlah pasangan konkordan (nc​) dan diskordan (nD​) dari total semua kemungkinan pasangan unik, yaitu $\left(\begin{array}{c}n\\ 2\end{array}\right)=\frac{n(n-1)}{2}$

1. Formula Utama (Tanpa Data Kembar)

   • Formula yang paling intuitif didasarkan pada selisih antara jumlah pasangan konkordan dan diskordan, dinormalisasi dengan total jumlah pasangan.

2. Langkah-langkah Perhitungan:

   • Ambil semua kemungkinan pasangan unik dari observasi Anda.
   • Untuk setiap pasangan, tentukan apakah itu konkordan atau diskordan.
   • Hitung jumlah total nc​ dan nD​.
   • Masukkan nilai-nilai ini ke dalam formula τ.

3. Penanganan Data Kembar (Ties)

   • Jika ada pasangan yang memiliki nilai yang sama (kembar) baik pada variabel X maupun Y, pasangan tersebut tidak dihitung sebagai konkordan maupun diskordan.
   • Dalam kasus ini, penyebut dalam formula disesuaikan untuk hanya mencakup pasangan yang tidak kembar.

Interpretasi dan Perbandingan dengan Spearman

Interpretasi Nilai τ:

• Sama seperti Spearman, nilai τ berkisar dari -1 hingga +1.
• +1: Semua pasangan adalah konkordan (korelasi positif sempurna).
• -1: Semua pasangan adalah diskordan (korelasi negatif sempurna).
• 0: Jumlah pasangan konkordan sama dengan diskordan (tidak ada asosiasi).

Perbedaan Utama dengan Spearman’s rs​:

1. Interpretasi Probabilistik: Ini adalah keunggulan terbesar Tau Kendall. Nilai τ memiliki interpretasi probabilistik langsung yang tidak dimiliki Spearman. Hubungannya dapat dijelaskan sebagai odds-ratio:

   • Di mana P(C) adalah probabilitas pasangan acak bersifat konkordan, dan P(D) adalah probabilitasnya bersifat diskordan.
   • Contoh: Jika $\tau =1/3,\frac{1+1/3}{1-1/3}=\frac{4/3}{2/3}=2$. Ini berarti, setiap pasangan pengamatan dua kali lebih mungkin untuk menjadi konkordan daripada diskordan. 5

2. Kompleksitas Komputasi: Untuk dataset besar, perhitungan Tau Kendall lebih intensif. Kompleksitasnya adalah O(n2), dibandingkan dengan Spearman yang lebih efisien yaitu O(nlogn).

Uji Hipotesis Sampel Besar

Untuk sampel yang cukup besar, kita bisa menggunakan aproksimasi normal untuk menguji hipotesis nol bahwa tidak ada korelasi di populasi (H0​:τ=0).

• Statistik Uji Z: ​​
• Prosedur: Nilai zτ​ yang dihitung kemudian dibandingkan dengan nilai kritis dari distribusi normal standar (misalnya, 1.96 untuk α=0.05 uji dua arah) untuk membuat keputusan menolak atau tidak menolak H0​.

Summary

• Tau Kendall (τ) adalah koefisien korelasi nonparametrik yang mengukur asosiasi dengan menghitung proporsi pasangan konkordan (searah) dan diskordan (berlawanan arah) dalam data. Keunggulan utamanya dibandingkan Spearman adalah interpretasi probabilistiknya yang jelas sebagai rasio peluang antara pasangan konkordan dan diskordan, meskipun secara komputasi lebih berat untuk dataset besar. Signifikansinya untuk sampel besar dapat diuji menggunakan statistik Z yang didekati dengan distribusi normal.

Additional Information (Optional)

Konteks Historis dan Teknis

• Maurice George Kendall (1907-1983) adalah seorang ahli statistik Inggris yang memberikan banyak kontribusi penting bagi teori statistik, termasuk pengembangan koefisien τ ini.
• Formula Formal: Definisi statistik yang lebih formal untuk τ adalah τ=n(n−1)2Sτ​​, di mana Sτ​=∑i<j​sign(ri​−rj​). Dalam notasi ini, kita terlebih dahulu mengurutkan data berdasarkan variabel pertama (X), lalu melihat tanda selisih peringkat dari variabel kedua (Y) untuk semua pasangan.

Aplikasi Praktis (Contoh 7.5 dari Kvam)

• Analisis Tren Penggunaan Air di Indiana: Tau Kendall digunakan untuk melaporkan tren penggunaan air di Indiana dari tahun 1986 hingga 1996. 7

• Pengambilan Air Permukaan (Surface Water): Hasilnya menunjukkan tidak ada tren yang jelas dari waktu ke waktu (p-value ≈ 0.59). 8 Ini berarti penggunaan air permukaan cenderung fluktuatif tanpa arah yang konsisten.

• Pengambilan Air Tanah (Ground-Water): Hasilnya menunjukkan tren peningkatan yang sedikit selama rentang 10 tahun tersebut (p-value ≈ 0.13). 9 Meskipun tidak signifikan pada level α=0.05 atau 0.10, p-value yang lebih rendah ini mengindikasikan adanya kecenderungan naik dalam penggunaan air tanah.