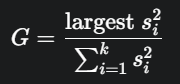Uji Cochran

Back to MA2281 Statistika nonparametrik

Topic

Questions/Cues

• Apa itu Uji Cochran?
• Apa batasan utama dari uji ini?
• Kapan Uji Cochran sangat berguna?
• Bagaimana formula dan prosedurnya?
• Apa itu statistik G?
• Bagaimana aturan keputusannya?
• Bagaimana contoh perhitungan detailnya?

Tujuan dan Konsep Dasar

Uji Cochran adalah metode alternatif dari Uji Bartlett yang digunakan untuk menguji homogenitas ragam (kesamaan ragam) dari beberapa populasi. Uji ini dikenal karena prosedur komputasinya yang lebih sederhana.

• Batasan dan Kegunaan Spesifik:

  1. Batasan Utama: Prosedur Uji Cochran secara tegas terbatas pada situasi di mana ukuran sampel untuk semua kelompok adalah sama (n1​=n2​=…=nk​).
  2. Kegunaan Spesifik: Uji ini sangat berguna untuk mendeteksi jika terdapat satu ragam yang nilainya jauh lebih besar dibandingkan ragam-ragam lainnya.

• Hipotesis yang Diuji:

  • Sama seperti Uji Bartlett, hipotesis yang diuji adalah:
    • Hipotesis Nol (H0​): Ragam dari semua k populasi adalah sama.
    • Hipotesis Alternatif (H1​): Tidak semua ragam populasi sama.

Prosedur Uji dan Statistik (G)

Prosedur Uji Cochran berpusat pada statistik uji yang disebut G.

1. Statistik Uji (G):

   • Statistik ini dihitung sebagai rasio dari ragam sampel terbesar terhadap jumlah dari semua ragam sampel.

2. Langkah-langkah Perhitungan:

   • Pastikan semua kelompok memiliki ukuran sampel yang sama (n).
   • Hitung ragam sampel (si2​) untuk setiap k kelompok.
   • Identifikasi nilai ragam sampel yang paling besar.
   • Jumlahkan semua nilai ragam sampel.
   • Bagi ragam terbesar dengan jumlah total ragam untuk mendapatkan nilai G.

3. Aturan Keputusan:

   • Uji Cochran adalah uji sisi kanan.
   • Hipotesis nol tentang kesamaan ragam ditolak jika nilai statistik G yang dihitung lebih besar dari nilai kritisnya. $g>g_{\alpha }$
   • Nilai kritis gα​ diperoleh dari Tabel A.11, berdasarkan taraf signifikansi α, jumlah kelompok k, dan derajat kebebasan untuk setiap ragam sampel $(v=n-1)$.

Contoh Perhitungan Lengkap

Kita akan menggunakan Uji Cochran untuk memeriksa asumsi kesamaan ragam pada data penyerapan air oleh agregat beton (Contoh 13.1), di mana kita memiliki k=5 kelompok dan ukuran sampel yang sama, n=6.

• Konteks: k=5 kelompok (agregat), n=6 sampel per kelompok. Derajat kebebasan v=n−1=5. Taraf signifikansi yang digunakan adalah α=0.05.

• 1. Hitung Ragam Sampel (si2​):

  • s12​=12,134
  • s22​=2,303
  • s32​=3,594
  • s42​=3,319
  • s52​=3,455

• 2. Identifikasi Ragam Terbesar dan Hitung Jumlahnya:

  • Ragam sampel terbesar adalah s12​=12,134.
  • Jumlah dari semua ragam adalah ∑i=15​si2​=12134+2303+3594+3319+3455=24,805.
• 3. Hitung Statistik Uji G:

  G=24,80512,134​=0.4892

• 4. Keputusan:

  • Cari nilai kritis dari Tabel A.11 untuk α=0.05, k=5, dan v=5. Nilai kritisnya adalah g0.05​=0.5065.
  • Bandingkan nilai G hitung dengan nilai kritis: 0.4892 vs. 0.5065.
  • Karena 0.4892 tidak lebih besar dari 0.5065, kita gagal menolak H0​.
  • Kesimpulan: Asumsi kesamaan ragam untuk data agregat beton ini dianggap wajar.

Summary

• Uji Cochran adalah metode yang komputasinya sederhana untuk menguji kesamaan ragam, namun penggunaannya terbatas hanya untuk kasus dengan ukuran sampel yang sama di semua kelompok. Uji ini sangat efektif untuk mendeteksi adanya satu ragam yang jauh lebih besar dari yang lain (outlier) dengan menggunakan statistik G, yaitu rasio ragam terbesar terhadap total seluruh ragam. Hipotesis kesamaan ragam ditolak jika nilai G melebihi nilai kritisnya (uji sisi kanan).

Additional Information (Optional)

Perbandingan Langsung: Cochran vs. Bartlett

Fitur	Uji Cochran	Uji Bartlett
Ukuran Sampel	Wajib Sama	Bisa Sama atau Berbeda
Komputasi	Sangat Sederhana	Lebih Kompleks (melibatkan logaritma/pangkat)
Fokus Deteksi	Efektif untuk 1 ragam yang sangat besar	Lebih umum untuk perbedaan ragam secara keseluruhan
Arah Uji	Sisi Kanan (Right-tailed)	Sisi Kiri (Left-tailed)

Pentingnya Batasan Ukuran Sampel Sama

• Batasan ukuran sampel yang sama pada Uji Cochran bukanlah sekadar anjuran, melainkan sebuah keharusan. Distribusi statistik G dan nilai-nilai kritis yang ada di tabelnya diturunkan secara matematis dengan asumsi bahwa semua sampel memiliki ukuran yang sama. Menggunakan uji ini pada data dengan ukuran sampel yang berbeda akan menghasilkan kesimpulan yang tidak valid dan menyesatkan.