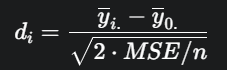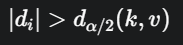Uji Dunnett

Back to MA2281 Statistika nonparametrik

Topic

Questions/Cues

• Apa tujuan spesifik Uji Dunnett?
• Bagaimana hipotesisnya berbeda dari Tukey?
• Bagaimana prosedur dan statistik ujinya?
• Bagaimana aturan keputusan untuk uji dua-sisi?
• Apakah uji ini bisa untuk uji satu-sisi?
• Bagaimana contoh perhitungannya?

Tujuan dan Konteks Penggunaan

Uji Dunnett adalah sebuah prosedur perbandingan ganda yang dikembangkan oleh C.W. Dunnett dengan tujuan yang sangat spesifik. Berbeda dengan Uji Tukey yang membandingkan semua kemungkinan pasangan rerata, Uji Dunnett digunakan ketika seorang peneliti hanya tertarik untuk membandingkan secara bersamaan setiap rerata perlakuan dengan satu rerata kontrol.

• Konteks:
  • Uji ini ideal untuk eksperimen yang memiliki kelompok referensi atau baseline, seperti kelompok plasebo dalam uji klinis, perlakuan “tanpa katalis” dalam reaksi kimia, atau metode standar yang ingin dibandingkan dengan metode-metode baru.
  • Tujuannya adalah untuk menentukan perbedaan signifikan antara setiap perlakuan dan kontrol tersebut pada satu taraf signifikansi gabungan (α).

Hipotesis dan Statistik Uji

• Hipotesis:

  • Secara umum, kita ingin menguji k hipotesis, di mana k adalah jumlah kelompok perlakuan (tidak termasuk kontrol).
  • $H_0:{\mu }_0={\mu }_i$​ (Rerata kontrol sama dengan rerata perlakuan ke-i)
  • $H_1:{\mu }_{}\ne \mu i$​ (Untuk uji dua-sisi)
  • … untuk i=1,2,…,k.
  • Di sini, ${\mu }_0$​ adalah rerata populasi untuk kelompok kontrol.

• Statistik Uji (di​):

  • Untuk setiap perbandingan perlakuan dengan kontrol, kita menghitung statistik di​
  • y​i.​: Rerata sampel untuk perlakuan ke-i.
  • y​0.​: Rerata sampel untuk kelompok kontrol.
  • MSE: Mean Square Error (s2) yang diperoleh dari tabel ANOVA yang mencakup semua kelompok (perlakuan + kontrol).
  • n: Ukuran sampel per kelompok (diasumsikan sama).

Aturan Keputusan dan Uji Satu-Sisi

• Uji Dua-Sisi (Two-Sided Test):

  • Aturan ini digunakan untuk mendeteksi apakah rerata perlakuan berbeda dari kontrol, tanpa mempedulikan arahnya (bisa lebih besar atau lebih kecil).
  • Kita menolak H0​ jika nilai absolut dari statistik di​ melebihi nilai kritisnya:
  • Nilai kritis dα/2​(k,v) diperoleh dari tabel statistik khusus untuk Uji Dunnett.
  • k adalah jumlah kelompok perlakuan (tidak termasuk kontrol).
  • v adalah derajat kebebasan untuk galat, yaitu N−(total kelompok)=N−(k+1).

• Uji Satu-Sisi (One-Sided Test):

  • Dalam banyak aplikasi praktis, peneliti tertarik pada perbedaan satu arah. Misalnya, apakah sebuah obat baru secara signifikan menurunkan kolesterol lebih baik dari plasebo (kontrol).
  • Untuk kasus ini, nilai kritisnya diperoleh dari tabel statistik Dunnett yang dirancang untuk uji satu-sisi.

Contoh Perhitungan Lengkap

Sebuah studi membandingkan efek 3 jenis katalis (k=3) terhadap hasil reaksi kimia, dengan satu kelompok tanpa katalis sebagai kontrol. Setiap kelompok memiliki n=5 observasi. Taraf signifikansi gabungan yang digunakan adalah α=0.05 (dua sisi). 4. Keputusan:

• Dari tabel statistik Dunnett, nilai kritis untuk uji dua-sisi dengan α=0.05, k=3 perlakuan, dan v=16 df adalah dkritis​=2.59.
• Bandingkan nilai absolut ∣di​∣ dengan 2.59: - ∣d1​∣=2.147<2.59 (Tidak signifikan) - ∣d2​∣=2.710>2.59 (Signifikan) - ∣d3​∣=2.147<2.59 (Tidak signifikan)
• Kesimpulan: Hanya rerata hasil reaksi untuk Katalis 2 yang secara signifikan berbeda dari rerata kelompok kontrol.

Summary

• Uji Dunnett adalah uji perbandingan ganda yang secara khusus dirancang untuk membandingkan beberapa rerata perlakuan terhadap satu rerata kontrol, sambil mempertahankan taraf signifikansi gabungan (experiment-wise error rate). Uji ini menggunakan statistik di​ untuk setiap perbandingan, dan perbedaan dianggap signifikan jika statistik tersebut melebihi nilai kritis yang diperoleh dari tabel khusus Dunnett, yang tersedia untuk uji satu-sisi maupun dua-sisi.

Additional Information (Optional)

Kapan Memilih Dunnett vs. Tukey?

• Gunakan Uji Tukey jika pertanyaan penelitian Anda adalah “Apakah ada perbedaan di antara semua kemungkinan pasangan perlakuan?” (misalnya, membandingkan efektivitas 5 merk obat yang berbeda satu sama lain).
• Gunakan Uji Dunnett jika pertanyaan penelitian Anda adalah “Apakah salah satu dari perlakuan baru ini lebih baik/berbeda dari standar/kontrol yang ada?” (misalnya, membandingkan 4 obat baru dengan plasebo).
• Uji Dunnett umumnya memiliki kekuatan statistik (power) yang lebih tinggi daripada Uji Tukey untuk tugas spesifik membandingkan perlakuan vs. kontrol, karena ia hanya fokus pada sejumlah kecil perbandingan yang paling relevan.

Taraf Signifikansi Gabungan (Joint Significance Level)

• Ketika kita menetapkan α=0.05 dalam Uji Dunnett, ini berarti probabilitas untuk salah menyimpulkan bahwa setidaknya satu perlakuan berbeda dari kontrol (padahal sebenarnya tidak) adalah 5%. Ini berbeda dengan menguji setiap perbandingan secara terpisah pada α=0.05, yang akan menghasilkan experiment-wise error rate yang jauh lebih tinggi.