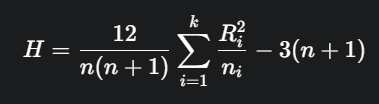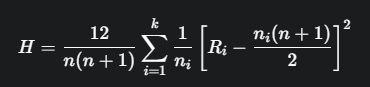Uji Kruskall-Wallis

Back to MA2281 Statistika nonparametrik

Topic

Questions/Cues

• Apa itu Uji Kruskal-Wallis (KW)?
• Apa bedanya dengan ANOVA biasa?
• Bagaimana prosedur uji KW?
• Bagaimana formula statistik H?
• Bagaimana aturan keputusannya?
• Bagaimana contoh perhitungannya?
• Apa yang dilakukan jika uji KW signifikan?

Tujuan dan Konsep Dasar

Uji Kruskal-Wallis (KW), atau sering disebut Uji H Kruskal-Wallis, adalah alternatif nonparametrik untuk analisis ragam (ANOVA) satu arah. Uji ini merupakan generalisasi atau perluasan dari Uji Jumlah Peringkat (Wilcoxon-Mann-Whitney) untuk kasus perbandingan tiga atau lebih (k>2) sampel independen.

• Perbedaan Utama dengan ANOVA:

  • Keunggulan utama Uji Kruskal-Wallis adalah tidak memerlukan asumsi bahwa data berasal dari populasi berdistribusi normal. ANOVA, di sisi lain, secara teoritis bergantung pada asumsi normalitas ini agar uji-F valid.
  • Karena bekerja dengan peringkat (ranks) dan bukan nilai data aktual, uji ini lebih kuat (robust) terhadap adanya pencilan (outliers).

• Hipotesis yang Diuji:

  • H0​: Sampel-sampel independen berasal dari populasi yang identik. Ini menyiratkan bahwa tidak ada perbedaan lokasi (median) antar kelompok.
  • H1​: Setidaknya ada dua sampel yang berasal dari populasi yang berbeda (berbeda dalam hal lokasi/median).

Prosedur dan Statistik Uji (H)

Prosedur Uji Kruskal-Wallis mengubah data numerik menjadi peringkat sebelum melakukan perhitungan.

1. Langkah-langkah Prosedur:

   • Gabungkan dan Peringkatkan: Gabungkan semua data dari k kelompok menjadi satu set data besar. Urutkan semua data dari yang terkecil hingga terbesar dan berikan peringkat dari 1 hingga n (total jumlah observasi).
   • Tangani Data Kembar (Ties): Jika ada nilai data yang sama, berikan peringkat rata-rata dari posisi yang seharusnya mereka tempati.
   • Jumlahkan Peringkat: Untuk setiap kelompok asli, jumlahkan peringkat dari observasi yang termasuk di dalamnya. Jumlah peringkat untuk kelompok ke-i dilambangkan dengan Ri​.

2. Statistik Uji (H):

   • Statistik H dihitung menggunakan formula berikut:

   • n adalah total jumlah observasi dari semua kelompok.

   • ni​ adalah jumlah observasi di kelompok ke-i.

   • Ri​ adalah jumlah peringkat di kelompok ke-i.

   • k adalah jumlah kelompok/sampel.

3. Aturan Keputusan:

   • Distribusi statistik H dapat didekati dengan baik oleh distribusi Khi-Kuadrat (χ2) dengan derajat kebebasan v=k−1.
   • Aproksimasi ini dianggap baik jika ukuran setiap sampel (ni​) setidaknya 5.
   • Uji ini adalah uji sisi kanan. Nilai H yang besar menunjukkan penolakan H0​.
   • Kita menolak H0​ jika nilai H hitung lebih besar dari nilai kritis Khi-Kuadrat: h>χα2​(k−1).

Contoh Perhitungan Lengkap

Sebuah eksperimen membandingkan laju bakar propelan dari 3 sistem misil (k=3) dengan α=0.05. Ukuran sampel tidak sama: n1​=5,n2​=6,n3​=8, sehingga total n=19.

1. Peringkat dan Jumlahkan Peringkat: Setelah semua 19 data digabungkan dan diperingkatkan (termasuk menangani data kembar), jumlah peringkat untuk setiap sistem misil adalah:

   • R1​=61.0
   • R2​=63.5
   • R3​=65.5

2. Hitung Statistik H:

3. Keputusan

   • Nilai kritis dari tabel Khi-Kuadrat untuk α=0.05 dan v=k−1=2 derajat kebebasan adalah 5.991.
   • Bandingkan nilai H hitung dengan nilai kritis: 1.66 vs. 5.991.
   • Karena 1.66 tidak lebih besar dari 5.991, kita gagal menolak H0​.
   • Kesimpulan: Tidak ada cukup bukti untuk menyatakan bahwa laju bakar propelan berbeda di antara ketiga sistem misil tersebut.

Summary

• Uji Kruskal-Wallis adalah alternatif nonparametrik untuk ANOVA satu arah, yang digunakan untuk membandingkan tiga atau lebih kelompok independen tanpa memerlukan asumsi normalitas data. Uji ini bekerja dengan mengubah semua data menjadi peringkat, kemudian menghitung statistik H berdasarkan jumlah peringkat di masing-masing kelompok. Statistik H ini dibandingkan dengan nilai kritis dari distribusi Khi-Kuadrat untuk menentukan apakah ada perbedaan signifikan antar kelompok.

Additional Information (Optional)

Formula Alternatif dan Koreksi Ties

• Formula H Alternatif: Terdapat bentuk formula H lain yang lebih intuitif karena menunjukkan perbandingan jumlah peringkat observasi (Ri​) dengan nilai harapannya di bawah H0​.
• Koreksi untuk Ties: Jika terdapat banyak data kembar, beberapa sumber menyarankan penggunaan formula terkoreksi (H′) untuk akurasi yang lebih tinggi, meskipun dalam banyak kasus perbedaannya kecil.

Perbandingan Ganda (Post-Hoc) setelah Uji KW

• Mirip dengan ANOVA, jika Uji Kruskal-Wallis signifikan (menolak H0​), itu hanya memberitahu kita bahwa setidaknya ada dua kelompok yang berbeda.
• Untuk mengetahui pasangan mana yang berbeda, diperlukan uji post-hoc nonparametrik. Salah satu metode yang diusulkan adalah membandingkan selisih rerata peringkat antara dua kelompok dengan nilai kritis yang didasarkan pada distribusi-t. Prosedur ini memungkinkan identifikasi spesifik kelompok mana yang berbeda secara signifikan satu sama lain.