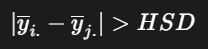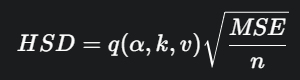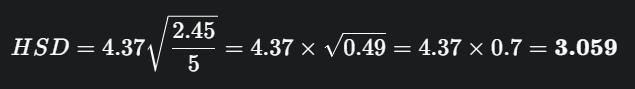Back to MA2281 Statistika nonparametrik
Topic
Questions/Cues
- Apa tujuan utama Uji Tukey?
- Mengapa uji t-test biasa tidak bisa digunakan?
- Apa itu Experiment-wise Error Rate?
- Bagaimana prosedur lengkap Uji Tukey?
- Apa itu statistik studentized range (q)?
- Bagaimana aturan keputusannya?
- Bagaimana contoh perhitungannya?
Tujuan dan Masalah Perbandingan Ganda
Uji Tukey, sering disebut juga Tukey’s Honestly Significant Difference (HSD) test, adalah sebuah uji post-hoc atau uji perbandingan ganda. Tujuannya adalah untuk mengidentifikasi pasangan rerata mana yang secara spesifik berbeda satu sama lain, setelah uji ANOVA secara keseluruhan menunjukkan hasil yang signifikan (yaitu, setelah kita menolak H0 bahwa semua rerata adalah sama).
- Masalah Penggunaan Uji-t Berulang Kali:
- Melakukan uji-t standar secara berulang untuk setiap pasangan rerata adalah tindakan yang tidak tepat.
- Alasannya adalah inflasi Galat Tipe I. Jika kita melakukan banyak perbandingan, masing-masing dengan taraf signifikansi α (misalnya, 0.05), probabilitas untuk membuat setidaknya satu kesalahan Tipe I (menyatakan ada perbedaan padahal tidak ada) di seluruh rangkaian perbandingan akan menjadi jauh lebih besar dari α.
- Experiment-wise Error Rate:
- Ini adalah probabilitas untuk membuat setidaknya satu Galat Tipe I dalam satu “keluarga” atau set perbandingan dalam satu eksperimen.
- Jika kita melakukan r perbandingan independen, laju galat ini dihitung sebagai: 1−(1−α)r.
- Contoh: Jika kita membandingkan k=4 rerata, ada r=6 kemungkinan perbandingan pasangan. Jika α=0.05, maka experiment-wise error rate-nya adalah 1−(0.95)6≈0.26 atau 26%, yang jauh lebih tinggi dari 5% yang diinginkan.
- Uji Tukey dirancang untuk mengontrol experiment-wise error rate ini pada level α yang kita tentukan.
Prosedur dan Aturan Keputusan Uji Tukey
Uji Tukey menggunakan satu nilai kritis tunggal untuk mengevaluasi semua selisih rerata pasangan.
Konsep Utama: Uji ini didasarkan pada distribusi rentang terstudentisasi (studentized range distribution). Statistik dari distribusi ini dilambangkan dengan q.
Aturan Keputusan: Perbedaan antara dua rerata sampel (yi. dan yj.) dianggap signifikan jika nilai absolut dari selisihnya melebihi nilai kritis yang disebut HSD (Honestly Significant Difference).
Formula HSD:
- q(α,k,v): Nilai kritis dari tabel studentized range (Tabel A.12).
- α: Taraf signifikansi experiment-wise yang diinginkan (misalnya 0.05 atau 0.01).
- k: Jumlah total kelompok/perlakuan yang dibandingkan.
- v: Derajat kebebasan untuk galat (N−k), diambil dari tabel ANOVA.
- MSE: Mean Square Error (Kuadrat Tengah Galat atau s2) dari tabel ANOVA.
- n: Ukuran sampel per kelompok (Uji Tukey standar mengasumsikan ukuran sampel sama).
Contoh Perhitungan Lengkap
Misalkan sebuah eksperimen memiliki k=6 perlakuan, dengan n=5 observasi per perlakuan. Dari tabel ANOVA, kita mendapatkan MSE=2.45 dengan v=24 derajat kebebasan.
1. Urutkan Rerata Sampel: Rerata sampel dari yang terkecil hingga terbesar adalah:
- y2.=14.50
- y5.=16.75
- y1.=19.84
- y3.=21.12
- y6.=22.90
- y4.=23.20
2. Tentukan Nilai Kritis (q) dan Hitung HSD:
- Untuk α=0.05, k=6, dan v=24, nilai dari Tabel A.12 adalah q(0.05,6,24)=4.37.
- Hitung nilai HSD:
3. Bandingkan Semua Selisih Pasangan dengan HSD:
- Selisih terbesar: ∣y4.−y2.∣=∣23.20−14.50∣=8.70. Karena 8.70>3.059, rerata 4 dan 2 berbeda signifikan.
- Selisih lain: ∣y6.−y2.∣=∣22.90−14.50∣=8.40. Karena 8.40>3.059, rerata 6 dan 2 berbeda signifikan.
- Lanjutkan untuk semua pasangan…
- Selisih terkecil antara rerata yang tidak bersebelahan: ∣y1.−y5.∣=∣19.84−16.75∣=3.09. Karena 3.09>3.059, rerata 1 dan 5 juga berbeda signifikan.
4. Kesimpulan: Buat daftar semua pasangan yang selisihnya melebihi 3.059. Berdasarkan contoh, ada 10 pasang rerata yang ditemukan berbeda signifikan.
Uji Tukey (HSD) adalah uji perbandingan ganda yang digunakan setelah ANOVA signifikan untuk mengidentifikasi pasangan rerata mana yang berbeda, dengan keunggulan utama mampu mengontrol experiment-wise error rate. Prosedurnya adalah menghitung satu nilai kritis tunggal (HSD) menggunakan statistik studentized range (q), kemudian membandingkan selisih absolut dari setiap pasangan rerata dengan nilai HSD tersebut. Jika selisihnya lebih besar dari HSD, pasangan rerata tersebut dianggap berbeda secara signifikan.
Additional Information (Optional)
Pendekatan Interval Kepercayaan
- Secara konseptual, Uji Tukey setara dengan membuat interval kepercayaan simultan untuk semua selisih pasangan rerata. Rumusnya adalah:
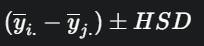
- atau
- Jika interval kepercayaan yang dihasilkan untuk sebuah pasangan tidak mencakup nol, maka kedua rerata tersebut dianggap berbeda secara signifikan pada taraf α. Ini memberikan cara lain untuk memvisualisasikan dan memahami hasil uji.
Asumsi
- Uji Tukey mengasumsikan hal yang sama dengan ANOVA, termasuk normalitas, independensi, dan homogenitas ragam. Versi standar dari Uji Tukey juga dirancang untuk ukuran sampel yang sama di setiap kelompok. Untuk ukuran sampel yang tidak sama, variasi yang lebih umum digunakan adalah uji Tukey-Kramer.