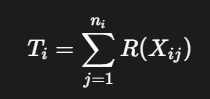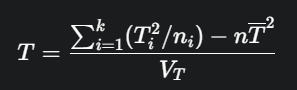Variance Test For Several Populations

Back to MA2281 Statistika nonparametrik

Topic

Questions/Cues

• Apa tujuan Uji Ragam Nonparametrik?
• Kapan uji ini digunakan?
• Bagaimana ide dasar di balik uji ini?
• Bagaimana prosedur lengkapnya?
• Bagaimana formula statistik T?
• Bagaimana aturan keputusannya?
• Apa yang dilakukan jika uji ini signifikan?

Tujuan dan Konsep Dasar

Uji Ragam Nonparametrik untuk Beberapa Populasi adalah sebuah metode untuk menguji hipotesis kesamaan ragam dari tiga atau lebih (k≥3) populasi. Uji ini merupakan perluasan dari Uji Conover (untuk dua populasi) dan memiliki struktur yang mirip dengan Uji Kruskal-Wallis.

• Konteks Penggunaan:

  • Ini adalah alternatif nonparametrik untuk uji parametrik seperti Uji Bartlett atau Cochran.
  • Uji ini sangat berguna ketika asumsi normalitas data tidak terpenuhi, yang membuat uji parametrik menjadi tidak dapat diandalkan.

• Hipotesis yang Diuji:

  • H0​: Ragam dari semua k populasi adalah sama $(H_0:{\sigma }_1^2={\sigma }_2^2=\cdots ={\sigma }_k^2)$
  • H1​: Setidaknya ada dua ragam populasi yang tidak sama.

Prosedur Uji: Peringkat pada Sebaran Data

Ide utama dari uji ini sangat unik karena tidak memberi peringkat pada data asli, melainkan pada ukuran sebarannya.

1. Hitung Deviasi Kuadrat: Untuk setiap observasi (Xij​) dalam setiap kelompok, hitung deviasi kuadrat dari rerata kelompoknya masing-masing: (Xij​−xi​)2. Nilai ini merepresentasikan seberapa jauh setiap titik data dari pusatnya, yang merupakan ukuran sebaran.
2. Gabungkan dan Peringkatkan: Kumpulkan semua nilai deviasi kuadrat dari semua kelompok menjadi satu set data besar, lalu berikan peringkat pada nilai-nilai ini dari yang terkecil hingga terbesar. Peringkat ini kita sebut R(Xij​).

Statistik Uji (T) dan Aturan Keputusan

Perhitungan statistik uji T memerlukan beberapa komponen berdasarkan peringkat yang telah dibuat.

• Komponen Perhitungan:

  • Jumlah Peringkat (Ti​): Untuk setiap kelompok ke-i, jumlahkan semua peringkat deviasi kuadrat yang berasal dari kelompok tersebut.
  • Rerata Jumlah Peringkat (T): Rerata dari seluruh jumlah peringkat.
  • Varian Peringkat (VT​): Ragam dari seluruh peringkat yang ada.

• Statistik Uji (T):

  • Statistik uji T dihitung menggunakan formula berikut

• Aturan Keputusan:

  • Di bawah hipotesis nol, statistik T mengikuti aproksimasi distribusi Khi-Kuadrat (χ2) dengan derajat kebebasan v=k−1.
  • Uji ini adalah uji sisi kanan. Nilai T yang besar mengindikasikan adanya perbedaan ragam.
  • Kita menolak H0​ jika nilai T hitung lebih besar dari nilai kritis Khi-Kuadrat: $T_{h}itung>{\chi }_{\alpha }^2(k-1)$.

Contoh Konseptual

Misalkan kita menguji kesamaan ragam dari hasil panen pada k=4 plot tanaman dengan total observasi n=34 dan α=0.05.

1. Peringkat Deviasi: Hitung (Xij​−xi​)2 untuk setiap dari 34 tanaman. Peringkatkan ke-34 nilai ini dari 1 sampai 34.
2. Jumlahkan Peringkat: Misalkan setelah dijumlahkan per kelompok, didapat: T1​=3845,T2​=4631,T3​=4032,T4​=1174.5.
3. Hitung Statistik T: Setelah menghitung komponen T dan VT​, misalkan didapat nilai statistik uji T=4.5086.
4. Keputusan:
   • Nilai kritis dari tabel Khi-Kuadrat untuk α=0.05 dan v=k−1=3 derajat kebebasan adalah 7.815.
   • Karena Thitung​=4.5086 tidak lebih besar dari 7.815, kita gagal menolak H0​.
   • Kesimpulan: Tidak ada bukti yang cukup kuat untuk menyimpulkan bahwa ragam hasil panen dari keempat plot tersebut berbeda.

Summary

• Uji ragam nonparametrik untuk beberapa populasi adalah metode untuk membandingkan kesamaan sebaran data dari tiga atau lebih kelompok, terutama ketika asumsi normalitas tidak terpenuhi. Uji ini secara unik bekerja dengan memberi peringkat pada nilai deviasi kuadrat setiap observasi dari rerata kelompoknya, bukan pada data aslinya. Statistik uji T yang dihasilkan kemudian dibandingkan dengan distribusi Khi-Kuadrat untuk menentukan apakah terdapat perbedaan ragam yang signifikan antar kelompok.

Additional Information (Optional)

Perbandingan Ganda (Post-Hoc)

• Jika hasil uji T signifikan (menolak H0​), artinya setidaknya ada dua ragam yang berbeda. Untuk mengetahui pasangan mana yang berbeda, dapat dilakukan uji perbandingan ganda.
• Prosedurnya adalah membandingkan selisih rerata peringkat (Ti​/ni​) antara dua kelompok dengan nilai kritis yang didasarkan pada distribusi-t. ​ni​Ti​​−nj​Tj​​​>Nilai Kritis

Efisiensi Relatif Asimtotik (A.R.E.)

• Efisiensi uji ini dibandingkan dengan uji parametrik standar bergantung pada distribusi data asli.
  • Untuk data normal, uji ini sedikit kurang efisien (A.R.E. = 0.76).
  • Namun, untuk data dengan ekor tebal (seperti distribusi double-exponential), uji ini bisa jauh lebih efisien dan lebih kuat (A.R.E. > 1.08).

Formula jika Tidak Ada Ties

• Jika tidak ada nilai deviasi kuadrat yang sama (tidak ada ties dalam peringkat), perhitungan beberapa komponen menjadi lebih sederhana:
  • T=6(n+1)(2n+1)​
  • VT​=180n(n+1)(2n+1)(8n+11)​